Poliedros são sólidos geométricos cujas superfícies são polígonos planos.
Observe os dois exemplos:
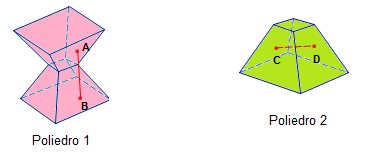
Em cada um dos poliedros, foi traçado um segmento de reta cujas extremidades são pontos de faces diferentes. Repare que no Poliedro 1 o segmento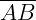 
fica na parte de “fora” (não interna) do poliedro. Isso não acontece no Poliedro 2, pois o segmento 
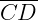ficou na parte de “dentro” (interna).
Considerando que um segmento de reta está contido num poliedro quando está de maneira completa na sua parte interna e/ou na sua superfície, podemos escrever a observação acima da seguinte forma:
O segmento 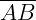não está contido no Poliedro 1, enquanto que o segmento 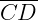está contido no Poliedro 2.
Um poliedro é convexo se dados quaisquer dois pontos pertencentes a superfície desse poliedro, o segmento que tem esses pontos como extremidades está inteiramente contido no poliedro. Caso exista algum segmento que não satisfaça essa condição, trata-se de um poliedro côncavo.
O Poliedro 1 é côncavo e o Poliedro 2 é convexo.
Observação: O segmento 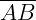não estando contido no Poliedro 1 prova que ele é côncavo, mas o segmento 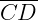estando contido no Poliedro 2 não prova que ele é convexo, pois para isso precisaríamos provar que TODOS os segmentos do tipo estão contidos. Portanto, a afirmação acima de que o Poliedro 2 é convexo foi dada sem qualquer demonstração, mesmo sendo verdadeira.
Relação de Euler
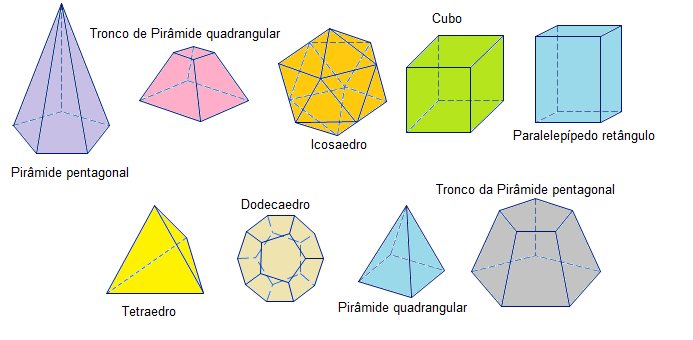
Observe os poliedros convexos e a tabela resumo de número de vértices, arestas e faces deles em seguida:
| Poliedro | Nº de faces (F) | Nº de Vértices (V) | Nº de arestas (A) |
| Pirâmide pentagonal | 6 | 6 | 10 |
| Tronco de pirâmide quadrangular | 6 | 8 | 12 |
| Icosaedro | 20 | 12 | 30 |
| Cubo | 6 | 8 | 12 |
| Paralelepípedo retângulo | 6 | 8 | 12 |
| Tetraedro | 4 | 4 | 6 |
| Dodecaedro | 12 | 20 | 30 |
| Pirâmide quadrangular | 5 | 5 | 8 |
| Tronco da pirâmide pentagonal | 7 | 10 | 15 |
Relação de Euler: Se, em um poliedro convexo, V é o número de vértices, F é o número de faces e A é o número de arestas, então vale a relação:
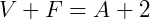
Observação: Todo poliedro convexo obedece à relação de Euler, já os poliedros côncavos podem obedecê-la ou não.
Veja se os dados da tabela satisfazem tal expressão. Você verá que sim!!
Poliedros regulares
Um polígono regular é aquele em que todos os seus lados possuem a mesma medida e todos os ângulos internos são congruentes entre si.
Considerando tal definição, observe a definição de poliedro regular:
Um poliedro é chamado regular se, e somente se:
- É convexo.
- Todas as suas faces são formadas por polígonos regulares e congruentes entre si.
- Todos os vértices formam ângulos congruentes.
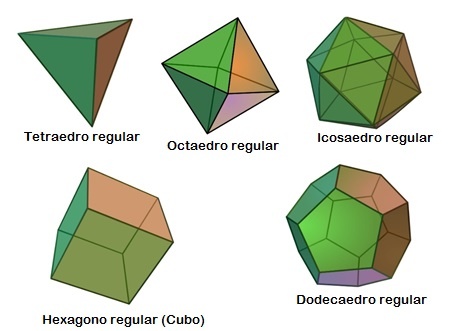
Existem 5, e somente 5, tipos de poliedros regulares. São eles:
Texto originalmente publicado em https://www.infoescola.com/matematica/poliedros-concavos-e-convexos/