O fenômeno da dilatação ocorre quando a temperatura de um corpo aumenta. As moléculas do corpo se agitam pela energia térmica recebida, se afastando umas das outras, o que provoca o aumento do tamanho do material. Quando a temperatura do corpo diminui, ele tende a se contrair. Isso é o que acontece com os nossos dedos, por exemplo. Nos dias frios eles se contraem e o anel fica largo. Nos dias quentes nossos dedos incham e o anel fica apertado.
A dilatação ocorre de três formas, dependendo da geometria do material:
- linear: ocorre em apenas uma dimensão, como barras, fios, arestas, etc.
- superficial: ocorre em duas dimensões, em superfícies (áreas), como chapas, face de um cubo, seção transversal de fios, entre outros.
- volumétrica: ocorre em três dimensões, aumentando o volume, como uma esfera, um cubo, ou qualquer outra forma volumétrica.
Aqui trataremos apenas da dilatação superficial. Contudo, antes é necessário lembrar da equação da dilatação linear, pois a utilizaremos nos cálculos posteriores. Ela é dada a seguir
ΔL = L1 . α . ΔT
ou ainda, se ΔL = L – L1,
L = L1 + L1 . α . ΔT
onde L1 é o comprimento inicial e ΔL a variação do comprimento depois de aquecido o material. Esta variação do comprimento depende de L1, da variação de temperatura sofrida ΔT e do coeficiente de dilatação linear α, característico de cada substância. Esta equação foi determinada experimentalmente e dela obtemos a dilatação superfial e volumétrica. Vamos ao cálculo da dilatação superfial.
Suponha uma chapa quadrada, cuja área seja A1 e suas dimensões L1. Se ela for aquecida, aumentando sua temperatura em ΔT, sua nova área será A e suas novas dimensões, maiores agora, serão L. Esta situação é representada na figura a seguir.
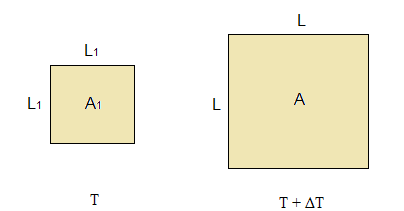
Figura 1. Dilatação de uma chapa quadrada.
Temos que as áreas inicial e final, respectivamente, serão:
A1 = L1 . L1 = (L1)² (1)
A = L . L = (L)² (2)
Utilizando a segunda equação da dilatação linear (L = L1 + L1.α.ΔT) para os lados da chapa quadrada dilatada, obtemos para a equação (2):
A = L . L = (L)² = (L1 + L1.α.ΔT)² = (L1)² + 2.(L1).(L1.α.ΔT) + (L1.α.ΔT)² =
= (L1)² + 2.(L1)². α.ΔT + (L1)².α².ΔT²
Como o coeficiente de dilatação linear de um material α é da ordem de 10-5, no caso de α² será da ordem de 10-10, que é um número muito pequeno, levando a anulação do termo (L1)².α².ΔT² no cálcula da área final A acima. Aplicando (1) também, resulta
A = (L1)² + 2.(L1)². α.ΔT + (L1)².α².ΔT²
A = A1 + 2.A1 .α.ΔT + 0
A = A1 + 2.A1 .α.ΔT
A – A1 = A1 .2α.ΔT
ΔA = A1 .2α.ΔT
Tomando o coeficiente de dilatação superficial β = 2α, temos
ΔA = A1.β.ΔT
Sendo esta a equação da dilatação superficial.
Texto originalmente publicado em https://www.infoescola.com/termodinamica/dilatacao-superficial/