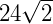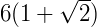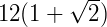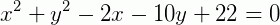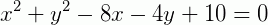Circunferência é a figura geométrica formada por todos os pontos que equidistam igualmente de um ponto fixo, chamado de centro. A essa distância entre o centro e cada ponto, chamamos de raio (r).
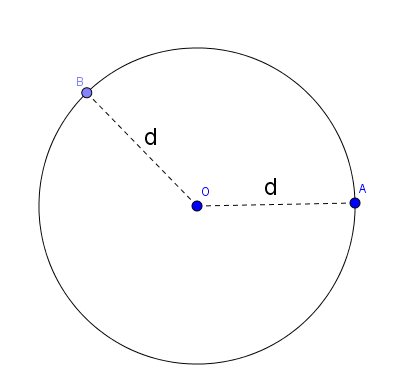
Matematicamente, uma circunferência 𝛌(O, r) é denotada por: 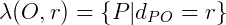 .
.
Assim, todos os pontos da circunferência têm a mesma distância ao centro. A distância do ponto A até o centro, por exemplo, é a mesma entre o ponto B e o centro.
Conteúdo deste artigo
Posição relativa de um ponto
Podemos determinar a posição de um ponto em relação à uma circunferência sem ter que “desenhar o ponto e a circunferência”.
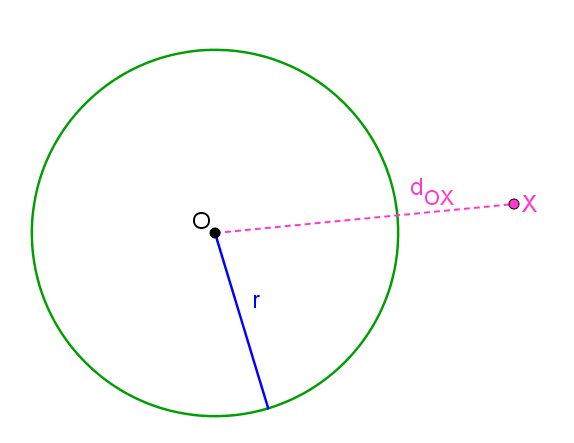
Um ponto pode ser interno, externo ou pertencer à circunferência. Vamos considerar um ponto x qualquer.
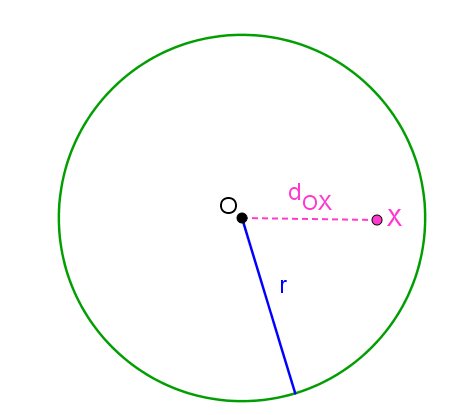
Se x é interno à circunferência, 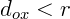 .
.
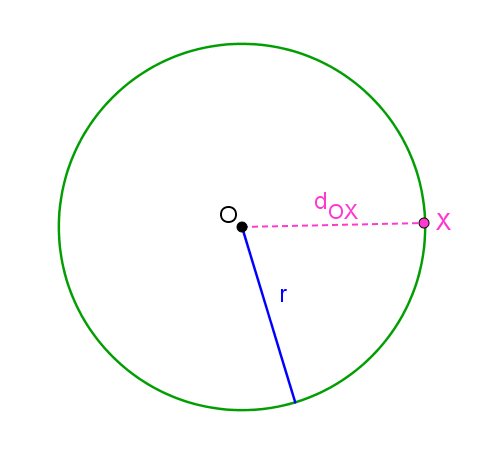
Se x pertence à circunferência, 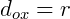 .
.
Se x é externo à circunferência, 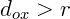 .
.
Interior e exterior
O conjunto de todos os pontos que estão fora da circunferência é chamado de seu “exterior”.
O conjunto de todos os pontos que estão dentro da circunferência é chamado de seu “interior”.
Assim, Considerando uma circunferência 𝛌(O, r), circunferência de centro O e raio r, podemos dizer que:
Interior: 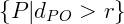
Interior: 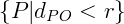
Onde P é um ponto qualquer que pode estar dentro ou fora da circunferência.
Corda, diâmetro e raio
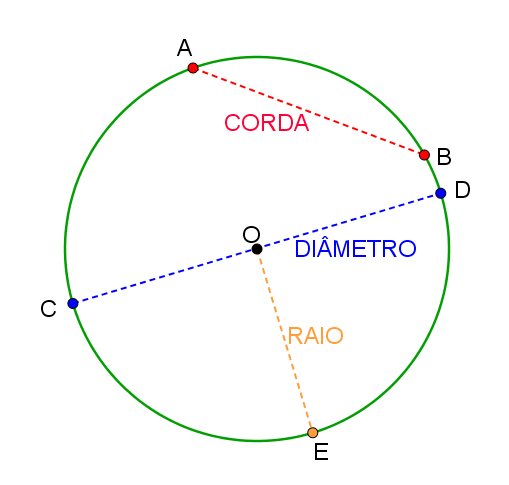
A corda de uma circunferência é o segmento que possui as duas extremidades pertencentes à circunferência. Na figura, AB é uma corda.
O diâmetro de uma circunferência é uma corda que passa pelo centro da circunferência. Na figura, CD é um diâmetro.
O raio de uma circunferência é um segmento que possui uma extremidade no centro e outra pertencente à circunferência. Em qualquer circunferência, o raio sempre será metade do diâmetro. Na figura, OE é um raio.
Arco de circunferência e semicircunferência
Dada uma circunferência qualquer e dois pontos A e B, que não podem ser as extremidades de um diâmetro, chamamos de arco o conjunto de pontos que pertencem a circunferência que estão entre A e B. Também é um arco o conjunto de pontos que estão entre B e A.
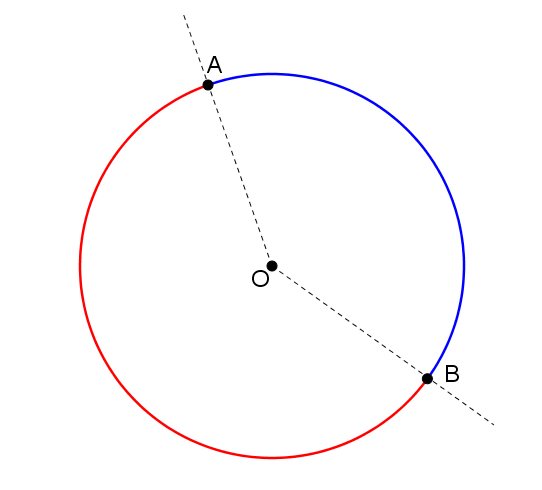
Podemos dizer que arcos são “pedaços” da circunferência. Uma circunferência com pontos A e B sempre delimitarão dois arcos, um maior e outro menor.
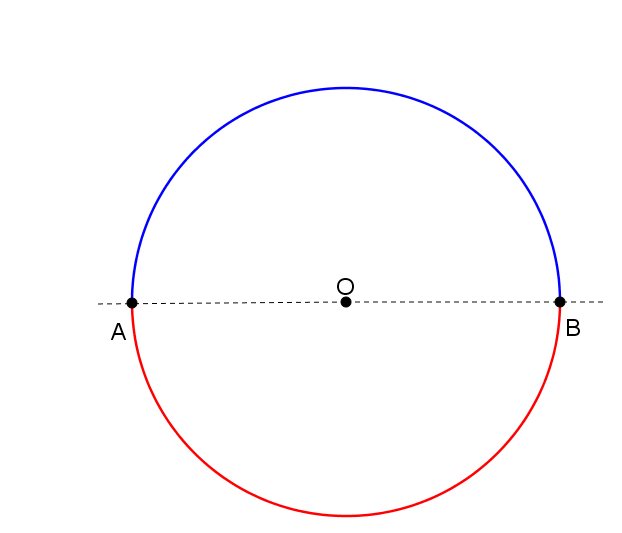
Quando os pontos A e B forem extremidades de um diâmetro, o arco será igual o arco e este arco damos o nome de semicircunferência.
Círculo
Podemos definir um círculo como sendo o conjunto de todos os pontos interiores de uma circunferência, ou seja, é o espaço contido dentro da circunferência.
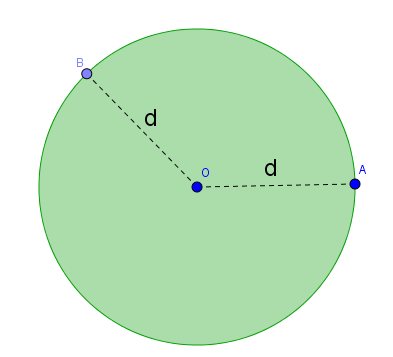
Assim, fica claro que:
- Circunferência: apenas a “linha” exterior.
- Círculo: circunferência mais o que está dentro dela.
Área de um círculo
A área de um círculo pode ser determinada matematicamente por:
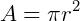
Onde r é a medida do círculo e um valor constante e usualmente igual a 3,14.
Setor circular
Um setor circular é uma região do círculo delimitada por dois de seus raios, partindo do centro e um arco
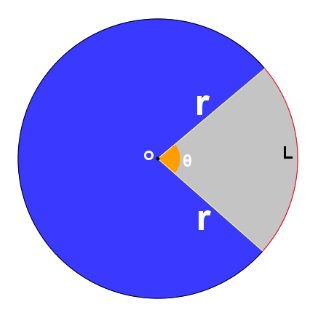
Usualmente podemos chamar um setor circular de “fatia de pizza”, pelo seu formato. O ângulo 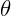 é chamado de ângulo central.
é chamado de ângulo central.
Observe que sempre temos dois setores circulares, um maior e outro menor (partes cinza e azul, respectivamente).
Para calcular a área de um setor circular, utilizamos as fórmulas:
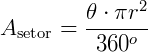
e
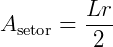
Onde na primeira, necessitamos do valor do ângulo e do raio do setor e na segunda, precisamos do raio e do comprimento do arco L do setor.
Perímetro de uma circunferência
Em qualquer circunferência, a razão entre a medida C do comprimento (perímetro) e a medida 2r de seu diâmetro (já que o diâmetro é o dobro do raio, ou o raio é metade do diâmetro) é constante. Ou seja, se pegarmos uma circunferência qualquer, a razão 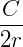 será sempre a mesma em qualquer outra circunferência.
será sempre a mesma em qualquer outra circunferência.
Esse valor constante, 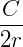 , é chamado de
, é chamado de 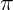 (Pi). Este número tem infinitas casas decimais, pois é um número irracional. Seu valor aproximado é 3,14159265... .
(Pi). Este número tem infinitas casas decimais, pois é um número irracional. Seu valor aproximado é 3,14159265... .
Usualmente consideramos que 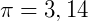 .
.
Então, partindo da igualdade 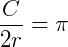 , concluímos que
, concluímos que 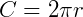 .
.
Então, o perímetro de uma circunferência, chamado apenas de comprimento, é determinado pelo produto do diâmetro (d = 2r) por 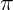 .
.
Exemplos
1. Qual o perímetro de uma circunferência cujo raio mede 3 cm?
Aplicando a fórmula:
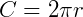
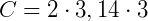
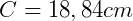
2. (Enem–2010). Uma fábrica de tubos acondiciona tubos cilíndricos menores dentro de outros tubos cilíndricos. A figura mostra uma situação em que quatro tubos cilíndricos estão acondicionados perfeitamente em um tubo com raio maior.
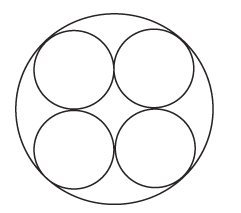
Suponha que você seja o operador da máquina que produzirá os tubos maiores em que serão colocados, sem ajustes ou folgas, quatro tubos cilíndricos internos. Se o raio da base de cada um dos cilindros menores for igual a 6 cm, a máquina por você operada deverá ser ajustada para produzir tubos maiores, com raio da base igual a
- A) 12 cm.
- b)
 cm.
cm. - C)
 cm.
cm. - D)
 cm.
cm. - E)
 cm.
cm.
Traçamos uma linha que será a diagonal do tubo maior, o segmento AB.
Note que os segmentos CE e ED tem, ambos 12 cm, já que são compostos de dois raios, um de cada tubo menor.
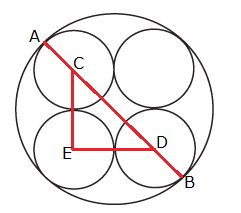
Assim, o diâmetro do tubo maior será CD + AC + DB.
Como AC e DB medem 6 cm, pois são raios, temos que a medida AB será:
AB = 12 + CD.
Para calcular CD, podemos usar o Teorema de Pitágoras:
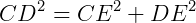
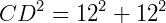
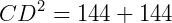
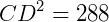
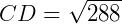
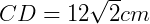
Assim,
AB = 12 + 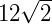 cm
cm
AB = 12(1 + 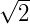 ) cm
) cm
Mas veja que o exercício pede o raio, então basta dividir AB por 2:
AB = 6(1 + 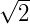 ) cm
) cm
Referências:
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.
RIBEIRO, Paulo Vinícius. Matemática: Ângulos na circunferência. Vol. 3. São Paulo: Bernoulli.
Texto originalmente publicado em https://www.infoescola.com/geometria-plana/circunferencia/