O Teorema de Cramer foi elaborado por Gabriel Cramer, e serve para acharmos a solução de qualquer sistema linear, com n equações e n incógnitas.
Exemplo de uma equação linear simples, com duas equações e duas incógnitas:
x+2y = 8
3x - y = 3
Fórmula
Para resolver um sistema linear com o teorema de Cramer, devemos calcular primeiro três valores: ∆p , ∆x e ∆y . Eles são encontrados da seguinte forma:
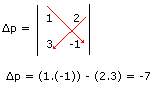
Perceba que, na tabela acima, as colunas correspondem aos valores que estão na frente das duas equações inicialmente dadas (os coeficientes de x e y). x por exemplo, ficará 1, 3x, ficará 3, 2y, ficará 2, e -y, ficará -1. Os números são colocados na posição igual à das equações, e multiplicados em "xis". O resultado da segunda multiplicação (2 . 3)deve ser subtraído da primeira (1 . (-1) . Então no final teremos, -7 para ∆p. Agora, temos que calcular ∆x e ∆y. É a mesma coisa, só que no lugar dos valores de x e y, colocamos os valores dos resultados das equações. Observe:
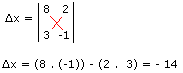
agora é a mesma coisa com o ∆y, trocamos os valores de y pelos resultados das equações:
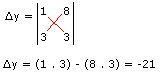
Agora, finalmente vamos descobrir os valores de x e y.
x = ∆x/∆p
logo:
x = -14 / -7 = 2
e y:
y = ∆y/∆p
logo:
y = -21 / -7 = 3
Para comprovar os resultados, basta trocar x e y por 2 e 3 nas equações dadas:
x+2y = 8
3x - y = 3
2+(2.3) = 2+6 = 8
(3.2) - 3 = 6 - 3 = 3
Texto originalmente publicado em https://www.infoescola.com/matematica/teorema-de-cramer-calculando-matrizes/