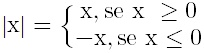Inequação Modular

O módulo de um número é igual a sua distância até zero. Sendo a grandeza distância sempre positiva, conclui-se que o módulo de um número é sempre positivo. Para encontrar o módulo de um número x, por exemplo, siga essa regra prática:

Por exemplo: |6| = 6, pois 6 > 0. Já |– 6| = – (– 6) = 6.

Agora que já relembramos o conceito de módulo, vamos ingressar nas inequações modulares.

Inequação modular é toda inequação cuja incógnita aparece em módulo. Veja alguns exemplos:

|x| > 6
|x| ≤ 4
|x + 3| > 7
|4x + 1| ≥ 3

Podemos utilizar as propriedades a seguir para resolver esse tipo de inequação:

|x| > a → x < – a ou x > a.
|x| < a → – a < x < a.
|x| ≤ a → – a ≤ x ≤ a.
|x| ≥ a → x ≤ – a ou x ≥ a.
|x – a| ≤ b → – b ≤ x – a ≤ b → a – b ≤ x ≤ a + b

Resolução de inequações modulares

Agora que você já conhece o conceito sobre inequações modulares e suas propriedades resolutivas, é hora de colocar a mão na massa. Antes de analisar as resoluções, tente resolver, utilizando as propriedades explanadas anteriormente, os modelos de inequações modulares acima. Veja as resoluções a seguir:

|x| > 6

x < – 6 ou x > 6

S = {x ∈ R | x < – 6 ou x > 6}

|x| ≤ 4

– 4 ≤ x ≤ 4

S = {x ∈ R | – 4 ≤ x ≤ 4}

|x + 3| > 7

x + 3 < – 7 ou x + 3 > 7

Se x + 3 < – 7, então:

x < – 7 – 3

x < – 10

Se x + 3 > 7, então:

x > 7 – 3

x > 4

S = {x ∈ R | x < – 10 ou x > 4}

|4x + 1| ≥ 3

4x + 1 ≤ – 3 ou 4x + 1 ≥ 3

Se 4x + 1 ≤ – 3, então:

4x ≤ – 3 – 1

4x ≤ – 4

x ≤ – 1

Se 4x + 1 ≥ 3, então:

4x ≥ 3 – 1

4x ≥ 2

x ≥ ½

S = {x ∈ R | x ≤ – 1 ou x ≥ ½}