Análise dimensional

Quando estudamos física, grandeza é o conceito mais básico que aprendemos, e que usamos para descrever fenômenos. No Sistema Internacional de Medidas (SI), as grandezas fundamentais, e suas respectivas unidades são: comprimento (metro – m), tempo (segundos – s), massa (quilogramas – kg), temperatura (Kelvin – K) e corrente elétrica (Ampère – A). Todas as outras grandezas e suas unidades resultam delas.

A análise dimensional é uma ferramenta que usamos para prever como uma grandeza física irá se comportar, sem precisar resolver um problema ou uma conta. Essa é uma ferramenta extremamente importante, pois nos permite: simplificar problemas, desenvolver intuição física e detectar erros, sem necessitar resolução da conta.

Sua principal característica é a homogeneidade dimensional, que quer dizer que todos os termos de uma equação/fórmula devem ter a mesma dimensão, ou, em outras palavras, elas devem ter as mesmas unidades envolvidas para que possam ser comparadas.

Para realizar o procedimento de análise dimensional devemos:

• Ter uma equação/fórmula (igualdade), de onde partimos, escrevendo as unidades de cada grandeza nessa equação;
• Manipulamos essas unidades como se elas fossem números (dividindo, multiplicando, etc.), a fim de encontrar as unidades da grandeza que queremos (lado esquerdo da igualdade).

Observações:

• A notação para representar a unidade de uma grandeza é: [grandeza]. Ex. tempo, representamos unidade como [t]=[s].
• Unidades compostas podem ser representadas como frações ou de forma linear. Ex. velocidade, [v]=[m/s] ou [m].[s]^-1.

Vejamos alguns exemplos de como realizar a análise dimensional.

Exemplos:

1) Determine a dimensão da grandeza física F, em 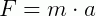$F=m\cdot a$, de acordo com o SI, sabendo que a é usado para designar a grandeza aceleração e m é usado para designar a grandeza massa.

Solução:

1) Vamos escrever as unidades de m e a no SI: 

$\left\lbrack F\right\rbrack =\left\lbrack m\right\rbrack \mathrm{.}\left\lbrack a\right\rbrack =\left\lbrack \mathit{kg}\right\rbrack \mathrm{.}\left\lbrack \frac{m}{{s}^{2}}\right\rbrack$

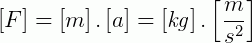
2) Como não há muito o que manipular entre essas unidades, podemos apenas reescrevê-las para expressão a unidade da grandeza F:

$\left\lbrack F\right\rbrack =\frac{\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack }\text{ ou }\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack \mathrm{.}{\left\lbrack {s}^{2}\right\rbrack }^{-1}$

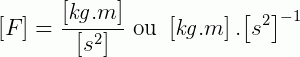
2) Determine a dimensão da grandeza X, em 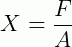$X=\frac{F}{A}$, de acordo com o SI, sabendo que F é usado para designar a grandeza força e que A é usado para designar a grandeza área (aqui uma área retangular de largura b e altura h).

Solução:

1) Para facilitar, vamos escrever as unidades de F e A, no SI, separadamente:

$\begin{cases}\left\lbrack F\right\rbrack =\left\lbrack m\right\rbrack \mathrm{.}\left\lbrack a\right\rbrack =\frac{\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack }\\ \left\lbrack A\right\rbrack =\left\lbrack b\right\rbrack \left\lbrack h\right\rbrack =\left\lbrack m\right\rbrack \mathrm{.}\left\lbrack m\right\rbrack =\left\lbrack {m}^{2}\right\rbrack \end{cases}$

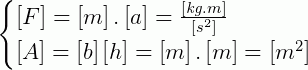
2) Vamos juntar isso na equação inicial e realizar algumas manipulações:

$\left\lbrack X\right\rbrack =\frac{\left\lbrack F\right\rbrack }{\left\lbrack A\right\rbrack }=\frac{\frac{\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack }}{\left\lbrack {m}^{2}\right\rbrack }=\frac{\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack }{\left\lbrack {s}^{2}\mathrm{.}{m}^{2}\right\rbrack }=\frac{\left\lbrack \mathit{kg}\right\rbrack }{\left\lbrack {s}^{2}\mathrm{.}m\right\rbrack }\text{ ou }\left\lbrack \mathit{kg}\right\rbrack \mathrm{.}{\left\lbrack {s}^{2}\mathrm{.}m\right\rbrack }^{-1}$

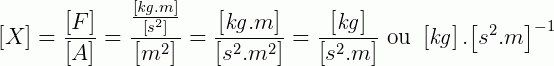
3) Determine qual deve ser a unidade da constante gravitacional G, na equação da Força gravitacional (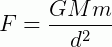$F=\frac{GMm}{d^2}$), onde, no SI, M e m são medida em quilogramas, d é medida em metros e F em Newton (1N=kg.m.s²).

Solução:

$F=\frac{\mathit{GMm}}{{d}^{2}}\rightarrow G=\frac{F{d}^{2}}{\mathit{Mm}}\rightarrow$

$\left\lbrack G\right\rbrack =\frac{\left\lbrack F\right\rbrack \left\lbrack {d}^{2}\right\rbrack }{\left\lbrack M\right\rbrack \left\lbrack m\right\rbrack }\rightarrow \left\lbrack G\right\rbrack =\frac{\left\lbrack \mathit{kg}\mathrm{.}\frac{m}{{s}^{2}}\right\rbrack \mathrm{.}\left\lbrack {m}^{2}\right\rbrack }{\left\lbrack \mathit{kg}\right\rbrack \left\lbrack \mathit{kg}\right\rbrack }\rightarrow$

$\left\lbrack G\right\rbrack =\frac{\left\lbrack \mathit{kg}\mathrm{.}m\right\rbrack \mathrm{.}\left\lbrack {m}^{2}\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack \left\lbrack \mathit{kg}\right\rbrack \left\lbrack \mathit{kg}\right\rbrack }\rightarrow \left\lbrack G\right\rbrack =\frac{\left\lbrack {m}^{3}\right\rbrack }{\lbrack kg\rbrack\cdot\lbrack s^2\rbrack}\text{ ou }$

$\lbrack G\rbrack=\lbrack m^3\rbrack\cdot\lbrack kg\rbrack^{-1}\cdot\lbrack s\rbrack^{-2}$

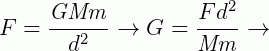
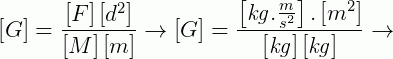
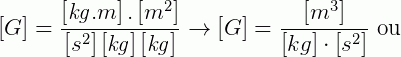
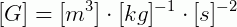
Mas análise dimensional não é usada apenas para determinar as unidades finais de uma grandeza, ela também pode ser utilizada quanto realizamos a conversão de unidades. Vejamos com um exemplo como fazer isso.

Exemplo

1) Escreva em m/s².

Solução:

Primeiro vamos lembrar que:

• 1 km = 1000m, ou seja, 1 [km] = 1000 [m]
• 1 h = 3600s, ou seja, 1 [h] = 3600 [s] → 1 [h²] = 12.960.000 [s²]

Agora basta alterarmos essa conversão nas unidades e manipular os valores numéricos, quando possível.

$a=35\frac{\mathit{km}}{h\mathrm{{^2}}}=35.\frac{\left\lbrack \mathit{km}\right\rbrack }{\left\lbrack {h}^{2}\right\rbrack }=35.\frac{1000\left\lbrack m\right\rbrack }{12960000\left\lbrack {s}^{2}\right\rbrack }=$

$\frac{35.1000}{12960000}\frac{\left\lbrack m\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack }={\mathrm{2,7.10}}^{-3}\frac{\left\lbrack m\right\rbrack }{\left\lbrack {s}^{2}\right\rbrack }$

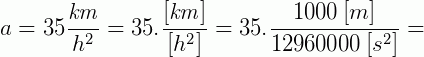
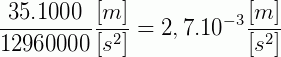
Referência:

TRANCANELLI, Diego. Grandezas físicas e análise dimensional: da mecânica à gravidade quântica. Revista Brasileira do Ensino Física. 38 (2). Junho, 2016. Disponível em: <https://www.scielo.br/j/rbef/a/z8ZCRv75nd3Q7jCc9VfL5NK/?lang=pt>. Acessado em: 12/01/2022.

Texto originalmente publicado em https://www.infoescola.com/fisica/analise-dimensional/