Quando um objeto encontra-se numa região onde atua um campo gravitacional, este sofre a ação da força peso, dada pelo produto de sua massa m pela respectiva aceleração gravitacional local, g. Geralmente, usa-se o módulo da aceleração gravitacional, uma vez que se sabe, a exemplo da Terra, que a aceleração gravitacional tem direção radial e nos sistemas de referências utilizados as grandezas positivas apontam do centro da Terra para fora, consequentemente, o campo gravitacional g é negativo para baixo. Desta forma temos, matematicamente, o módulo do peso do objeto dado pela equação:
P = m.g
Se considerarmos um objeto sobre uma superfície plana, teremos para cada partícula que constitui o referido corpo, uma força peso atuante. É o que expressa a equação:
ΣF = Σmi.g
Temos vários corpos de massa m. Mas podemos fazer o somatório de todas as forças que atuam sobre o corpo, e deste modo teremos uma equação para a força total atuante sobre o corpo em termos de sua massa total e a aceleração gravitacional local, expressa a seguir:
ΣF = g.Σmi = M.g
Para que este corpo esteja em equilíbrio estático, é necessário que esteja suspenso por uma tração T em algum ponto, ou com sua base apoiada sobre uma superfície, ou seja, apoiada vários pontos, conforme mostra a figura 01.
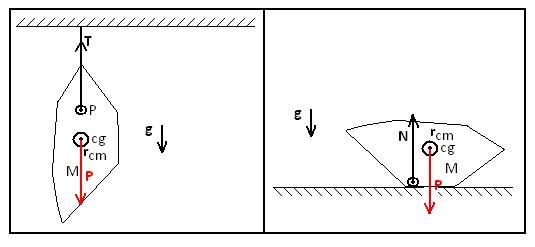Deste modo, na vertical, o somatório das forças seria nulo. Para um objeto sobre uma superfície teremos:
ΣF = N – g.Σmi = N – M.g = 0
E para o caso de um objeto suspenso por uma força de tração teremos:
ΣF = T – g.Σmi = T – M.g = 0
O torque resultante sobre o corpo é dado por:
Στ = Σ(ri x mi.g) = Σ(mi.ri x g) = M.rcm x g = rcm x Mg
A quantidade mi.ri , expressa em função das massas das partículas que constituem o corpo, mi, e das respectivas posições ocupadas por cada uma, ri, pode ser escrita em função da massa total M e da posição do centro de massa rcm conforme mostrado na figura 02.
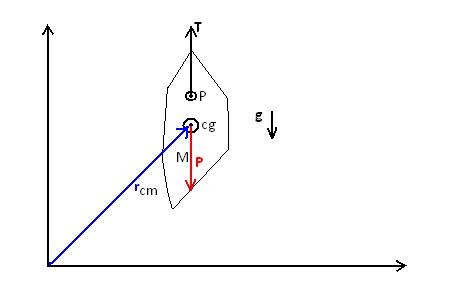Para uma condição de equilíbrio o somatório dos torques em relação ao centro de massa tem de ser nulo. Ou seja, matematicamente, teremos:
Στ = rcm x Mg = 0
Desta forma, todas as porções de massa que estiverem fora da base de apoio, aplicarão um torque sobre em torno extremidade da respectiva base de apoio.
Para determinar o centro de massa rcm de um objeto plano é muito simples: basta suspendê-lo em um ponto, por uma força de tração criada por um fio, por exemplo e riscar desde o ponto de suspensão até a extremidade inferior do objeto, como para determinar o centro de gravidade. Depois, escolhe-se outro ponto de suspensão em um dos lados, esquerdo ou direito do corpo, aproximadamente à meia altura. Novamente, risca-se na vertical. Na intersecção entre os dois riscos, ou seja, no cruzamento das linhas, localiza-se o centro de massa do objeto, mostrado na figura 03.
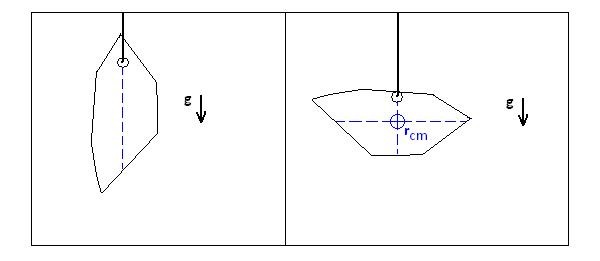Se for um objeto ao qual seja necessário considerar as três dimensões, é necessário efetuar mais um risco, perpendicular aos outros dois, num terceiro eixo de coordenadas considerado para aquele objeto. Neste caso, teremos um ponto localizado no interior do objeto, dependendo de sua forma. Para alguns casos, o centro de massa está fora do volume preenchido pelo objeto. Por exemplo, o centro de gravidade de um objeto de determinada substância e em forma de anel é localizado aproximadamente no centro, na região vazia.
Referências bibliográficas:
HALLIDAY, David, Resnik Robert, Krane, Denneth S. Física 1, volume 1, 4 Ed. Rio de Janeiro: LTC, 1996. 326 p.
Texto originalmente publicado em https://www.infoescola.com/fisica/centro-de-gravidade/