Normalmente, a dilatação em um volume sólido é mais difícil de se perceber do que em um volume líquido. Os sólidos se dilatam com menos facilidade que os líquidos. No entanto, não menos importante, a dilatação dos sólidos podem causar danos e até acidentes, se não observada e cuidada.
A resina, colocada pelo dentista, precisa ter o mesmo coeficiente de dilatação do dente, para não vir a quebrá-lo ao se dilatar. O espaçamento deixado em placas de concreto nas ruas e nos trilhos dos trens, o comprimento a mais nos fios de postes, enfim, sempre se procura compensar a dilatação ou a contração, que faz o sólido aumentar ou diminuir seu tamanho.
A dilatação pode ocorrer nos sólidos, nos gases, nos líquidos e até no plasma. Sabemos que ela pode ser linear, caso aconteça em uma dimensão, e superficial, se ocorrer em duas dimensões (áreas). Aqui trataremos da dilatação volumétrica (três dimensões), em especial nos corpos sólidos, visto que nos líquidos e nos gases são tratadas em outros artigos.
Considere um cubo sólido de volume inicial V1, logo, com as três dimensões L1 iguais. Se é aumentada a sua temperatura em ΔT, ele ficará com cada uma das dimensões maiores, L agora, e consequentemente com um volume maior (V). Veja a figura a seguir.
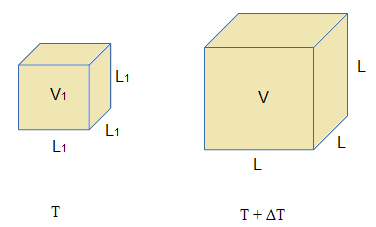
Figura 1. Dilatação volumétrica de um cubo sólido.
As arestas deste cubo aumentam conforme a dilatação linear, logo L obedecerá a equação:
L = L1 + L1.α. ΔT
Se o volume inicial é dado por
V1 = L1 . L1 . L1 = (L1)³ (1)
Vamos ao cálculo do novo volume após a dilatação volumétrica:
V = L . L . L = (L1 + L1.α. ΔT) . (L1 + L1.α. ΔT) . (L1 + L1.α. ΔT) (2)
onde substituímos a equação da dilatação linear em cada dimensão L do cubo dilatado.
Pela equação da dilatação superficial, sabemos que
L² = L . L = (L1 + L1.α. ΔT) . (L1 + L1.α. ΔT) = (L1)² + 2.(L1)². α.ΔT (3)
Substituindo (3) em (2), facilitamos os cálculos,
V = L . L . L = L² . L = [ (L1)² + 2.(L1)². α.ΔT ] . (L1 + L1.α. ΔT)
V = (L1)³ + (L1)³.α. ΔT + 2.(L1)³.α.ΔT + 2.(L1)³. α².ΔT²
Como o coeficiente de dilatação linear de um material α é da ordem de 10-5, no caso de α² será da ordem de 10-10, que é um número muito pequeno, levando a anulação do termo 2.(L1)³.α².ΔT². Assim
V = (L1)³ + (L1)³.α. ΔT + 2.(L1)³.α.ΔT + 2.(L1)³. α².ΔT²
V = (L1)³ + 3.(L1)³.α. ΔT + 0
V = (L1)³ + 3.(L1)³.α. ΔT
Substituindo (1) na equação acima e tomando o coeficiente de dilatação volumétrica γ = 3.α, temos
V = (L1)³ + 3.(L1)³.α.ΔT
V = V1 + V1 . 3.α.ΔT
V = V1 + V1.γ.ΔT
Esta é a equação que calcula a dilatação volumétrica. Como ΔV = V – V1, ela pode ser também escrita da seguinte forma
ΔV = V1.γ.ΔT
Se notarmos, os coeficientes de dilação linear (α), superficial (β) e volumétrico (γ) se relacionam da seguinte forma:
β = 2.α γ = 3.α
Leia também:
Texto originalmente publicado em https://www.infoescola.com/fisica/dilatacao-volumetrica/