Existe uma força de atração, proveniente da Terra, que faz com que os objetos e pessoas permaneçam na superfície terrestre. Também permite que a atmosfera fique em torno do Planeta, favorecendo as condições de vida, bem como satélites artificiais e natural (Lua).
Ao contrário do que muitos pensam, que apenas os corpos são atraídos pela Terra, a Terra também pode ser atraída por eles, visto que todos os corpos no universo possuem campo gravitacional. Mas a Terra nem sequer sente este campo gravitacional dos corpos que estão nela, pois quanto menor a massa do corpo, menor o campo, e quanto maior a massa, maior o campo.
Por este motivo que os corpos que estão na Terra, com massa infinitamente menor que a dela, sentem a força de atração de forma mais intensa, se movimentando em direção à Terra. Por isso os objetos caem!
Galileu Galilei (1564-1642) foi um dos primeiros a investigar experimentalmente a queda livre de objetos, descobrindo que corpos caiam com um movimento acelerado, com a aceleração constante. Posteriormente, Isaac Newton (1642-1727), físico inglês, cujo nascimento foi no mesmo ano em que Galileu faleceu, veio a desenvolver as teorias deste.
Newton comprovou a ideia de que todos os corpos possuem campo gravitacional, mas que pela grande massa, a força de atração de alguns prevalece, como é o caso da Terra. Newton chegou a seguinte conclusão, conhecida como a Lei da Gravitação Universal:
A força gravitacional entre dois pontos materiais tem intensidade diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que os separa.
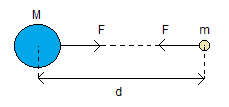
Figura 1. Forças iguais, de ação e reação, definem a atração entre corpos. Todos possuem campo gravitacional.
Matematicamente:
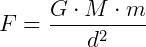
Por meio desta lei, podemos determinar a aceleração da gravidade g na superfície da Terra.
Se G = 6,7 . 10-11 N.m²/kg² (constante de gravitação universal) e considerando:
- F = m . a (segunda Lei de Newton)
- a = g (aceleração da gravidade)
- a massa da Terra M = 5,98 . 1024 kg
- o raio da Terra R = 6,35 . 106 m
Para qualquer corpo próximo a superfície da Terra (d = R):
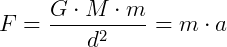
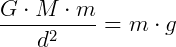
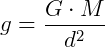
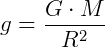
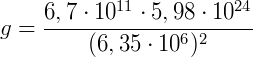
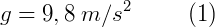
Este é o valor da aceleração da gravidade, constante, na superfície terrestre.
Notamos na equação que este valor de g independe da massa m, pois como é uma força de campo, (gravitacional no caso) depende apenas da massa do corpo que atrai e da distância do mesmo. Quanto mais longe do centro da Terra, menor a força da gravidade, assim como ocorre no campo elétrico.
A energia potencial gravitacional se deve a este campo gravitacional. Como há uma força de atração, ao afastarmos um objeto da superfície terrestre, a tendência é de que o corpo seja atraído de volta para a superfície. É necessário uma força externa para separar o objeto da superfície, esta força gera uma energia potencial, a qual será transformada totalmente em trabalho ao final da queda livre, pela conservação de energia.
Vamos ao cálculo desta energia potencial gravitacional agora!
Suponhamos que um objeto de massa m seja levantado a uma altura h da superfície, acumulando uma energia potencial gravitacional Ep g. Como ela será transformada totalmente em trabalho τ, pela conservação de energia, podemos escrever:
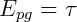
Sabemos que o trabalho é a força pelo deslocamento, se ambos estão no mesmo sentido (força para baixo e deslocamento também, veja figura 2).
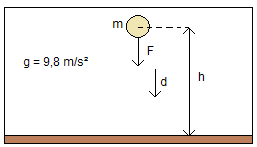
Figura 2. Corpo de massa m levantado a uma altura h, acumulando energia potencial para a queda.
Assim,
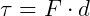
e pela segunda Lei de Newton, sabemos
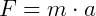
Tomando a = g,
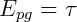
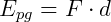
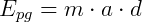
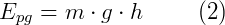
Esta é a equação da energia potencial gravitacional, onde g é a aceleração da gravidade, no valor de 9,8 m/s² na superfície da Terra, e Epg é dado em Joules (J).
Lembremos que em outro planeta ou qualquer corpo celeste, o valor de g é modificado. Na lua, por exemplo, g = 1,62 m/s², e em Marte g = 3,71 m/s². Basta usar a massa e o raio do respectivo corpo ao invés dos valores medidos para o Planeta Terra na equação (1).
Texto originalmente publicado em https://www.infoescola.com/fisica/energia-potencial-gravitacional/