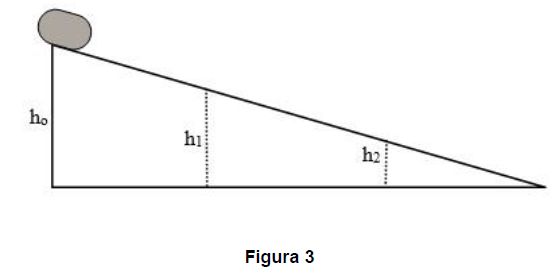
Quando um objeto se encontra sobre um plano inclinado, sofre a ação de uma força de reação normal ao apoio, conforme figura 01.

Neste caso foi desprezada a força de atrito. A força peso age na vertical, dirigida para o centro da Terra (de cima para baixo). Fixemos um plano cartesiano de coordenadas com o eixo x paralelo ao plano inclinado e o eixo y apontando para a direção da força normal, perpendicular a este plano. A força resultante na direção x é Px e pode ser escrita em função do ângulo θ. Então se obtém:
Px = P.senθ
A força normal tem o mesmo módulo de Py:
N = Py
Se
Py = P.cosθ
Então
N = P.cosθ
Ou seja, neste sistema de referência adotado, a força peso é representada por duas componentes, Px na direção x ou horizontal e Py na direção y ou vertical.
Fica evidente que quando o ângulo de inclinação do plano em relação à horizontal for maior, maior será a intensidade da componente da força peso na direção x, e menor será a intensidade da componente da força atuante na direção y, até um limite máximo, onde o ângulo for de 90º. Neste caso, a componente Px é igual ao peso P e a componente Py vale 0. Isso pode ser demonstrado:
Para a componente x:
Px = P.sen90º
Logo
Px = P.1
Pois
sen90º = 1
E obtemos:
Px = P
Para a componente y:
Py = P.cos90º
Logo,
Py = 0
Pois
cos90º = 0
Conforme havíamos comentado anteriormente.
Referências bibliográficas
HALLIDAY, David, RESNIK Robert, KRANE, Denneth S. Física 1, volume 1, 4 Ed. Rio de Janeiro: LTC, 1996. 326 p.
Texto originalmente publicado em https://www.infoescola.com/fisica/forcas-sobre-um-objeto-no-plano-inclinado/