Movimento Circular Uniformemente Variado

Mesmo que mantenha sua velocidade angular constante, há uma força resultante mantendo esse movimento. De acordo com a Segunda Lei de Newton, a essa força está associada uma aceleração – no caso, centrípeta. Ou seja, na comparação com o Movimento Uniforme, mesmo que a princípio pareça contraditório, o Movimento Circular e Uniforme é, de fato, uniforme justamente por haver um tipo de aceleração que permite que isso ocorra. A aceleração centrípeta é dada por:

$\vec{a}_{cp} = \frac{v^2}{R}$

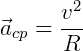
Onde:

• v é a velocidade escalar do objeto
• R é o raio da circunferência descrita.

Como a aceleração centrípeta tem direção e sentido, é uma grandeza vetorial.

Da relação

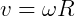
Podemos reescrever a aceleração centrípeta como:

$\vec{a}_{cp} = \frac{(\omega R)^2}{R}$

$\vec{a}_{cp} = \omega^2 R$

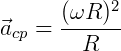
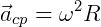
No entanto, também é possível que o objeto se mantenha em trajetória circular e tenha velocidade angular variável ao longo da trajetória. Assim, a aceleração angular média é a variação da velocidade angular no intervalo de tempo.

A aceleração calculada dessa forma é chama de aceleração angular média porque entre o intervalo de tempo usado, a velocidade pode apresentar valores diferentes do final ou do inicial. No entanto, se aproximarmos os instantes final e inicial cada vez mais, maiores são as chances de a velocidade sofrer variações cada vez menor. Assim, o Δt fica cada vez menor, cada vez mais próximo de 0 (mas nunca sendo 0, em absoluto). Teremos então a aceleração escalar instantânea.

$\gamma_m = \frac{\Delta \omega}{\Delta t}$

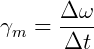
Aceleração angular média

$\displaystyle \gamma = \lim_{\Delta t \to 0}\frac{\Delta \omega}{\Delta t}$

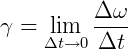
Aceleração angular instantânea (lê-se limite de Δt tendendo a zero).

Da relação entre grandezas escalar e angular (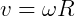$v = \omega R$), temos:

$\Delta v = \Delta \omega R$

$a_m = \frac{\Delta v}{\Delta t}$

$\gamma_m = \frac{\Delta \omega}{\Delta t}$

$\frac{\Delta v}{\Delta t} = \frac{\Delta \omega}{\Delta t} \cdot R$

$a = \gamma R$

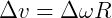
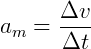
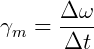
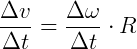
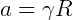
Ou

$\gamma = \frac{a}{R}$

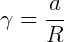
Assim, podemos estabelecer uma relação entre as grandezas escalar e angular nas equações horárias de seus respectivos movimentos:

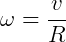
Função horária da velocidade:

$v = v_0 + a \cdot t$

$\frac{v}{R} = \frac{v_0}{R} + \frac{a}{R} \cdot t$

$\omega = \omega_0 + \gamma \cdot t$

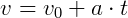
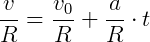
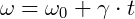
Função horária angular da velocidade

Função horário do espaço:

$S = S_0 + v_0 \cdot t + \frac{a}{2} \cdot t^2$

$\frac{S}{R} = \frac{S_0}{R} + \frac{v_0}{R} \cdot t + \frac{a}{2R} \cdot t^2$

$\theta= \theta_0 + \omega_0 \cdot t + \frac{\gamma}{2}\cdot t^2$

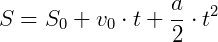
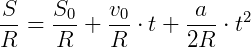
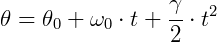
Função horária angular do espaço

Equação de Torricelli:

$v^2 = v_{0}^2 + 2 \cdot a \cdot \Delta S$

$\frac{v^2}{R} = \frac{v_{0}^2}{R} + 2 \frac{a}{R} \cdot \Delta S$

$\omega^2 = \omega_{0}^2 + 2\gamma\Delta S$

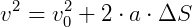
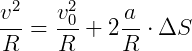
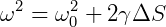
Equação de Torricelli para o Movimento Circular Uniformemente Variado (MCUV)

Referências:

Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016

Texto originalmente publicado em https://www.infoescola.com/fisica/movimento-circular-uniformemente-variado/