A terceira lei de Kepler foi a última das três notáveis contribuições à astronomia moderna devidas ao astrônomo e matemático alemão Johannes Kepler (1571-1630) no início do século XVII. Publicada em 1619, cerca de dez anos após a primeira e a segunda leis, na obra Harmonia do Mundo, a terceira das leis keplerianas é o ponto culminante do colossal trabalho de Kepler junto à abundante base de dados observacionais reunidos pelo astrônomo dinamarquês Tycho Brahe (1546-1601).
Em oposição à forma como chegou às suas duas primeiras leis, resultantes de um caminho essencialmente tortuoso, permeado de intuição e de suposições geométricas, a terceira lei foi derivada por Kepler a partir de uma busca obstinada e com grande rigor matemático em torno da ideia da existência de uma conexão entre o tempo que um planeta leva para completar sua órbita, denominado período orbital ou período sideral, e sua distância ao Sol. Após anos de tentativa e erro, Kepler finalmente obteve a relação que tanto perseguia.
A hoje denominada terceira lei de Kepler para o movimento planetário, também conhecida como “lei harmônica” ou “lei dos períodos”, afirma que:
O quadrado do período orbital de um planeta é diretamente proporcional ao cubo de sua distância média ao Sol.
Em termos matemáticos, representando por T o período orbital de um certo planeta e por r sua distância média ao Sol (que equivale ao comprimento do semieixo maior da órbita), a terceira lei de Kepler pode ser expressa pela equação abaixo:
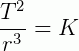
sendo K uma constante que possui o mesmo valor para as órbitas de todos os planetas do Sistema Solar. Se aplicada para órbitas de outro sistema planetário, a equação fornece um outro valor para K, que é, por sua vez, o mesmo para todas as órbitas daquele sistema. A quantidade K é denominada “constante de Kepler” em homenagem ao astrônomo que a descobriu.
A forma mais conveniente da constante de Kepler é obtida por meio da aplicação da lei ao caso da Terra. Se a distância r for medida em unidades astronômicas (UA), que é uma unidade de medida de distância equivalente à distância média da Terra ao Sol, e o período orbital T for medido em anos, os respectivos valores correspondentes à Terra serão r = 1 UA e T = 1 ano. Aplicada a terceira lei de Kepler, a constante K assume o valor 1 e a relação fica resumida à expressão:
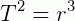
que pode ser aplicada a todos os planetas do Sistema Solar, desde que as distâncias sejam fornecidas em unidades astronômicas e os períodos orbitais, em anos. Essa relação é muito útil para a determinação de parâmetros orbitais dos planetas, pois basta que seja conhecido o período, por exemplo, para que se determine o semieixo maior de uma certa órbita, e vice-versa.
A tabela a seguir exibe os valores dos períodos orbitais e das distâncias médias ao Sol de cada um dos planetas visíveis a olho nu, os únicos conhecidos à época de Kepler. As unidades de medida utilizadas tornam K igual a 1 e os valores dos quadrados dos períodos e dos cubos das distâncias também são exibidos, permitindo que se verifique a acurácia da terceira lei de Kepler.
| Planeta | Período (anos) | Semieixo maior (UA) | T² | r³ |
| Mercúrio | 0,241 | 0,387 | 0,058 | 0,058 |
| Vênus | 0,615 | 0,723 | 0,378 | 0,378 |
| Terra | 1,000 | 1,000 | 1,000 | 1,000 |
| Marte | 1,881 | 1,524 | 3,537 | 3,537 |
| Júpiter | 11,862 | 5,203 | 140,7 | 140,8 |
| Saturno | 29,456 | 9,534 | 867,7 | 867,9 |
De modo bastante estrito, o conjunto das leis de Kepler é plenamente verdadeiro somente se o corpo central estiver fixo. Como posteriormente demonstrado por Isaac Newton, esse não é o caso de dois corpos que se atraem mutuamente por interação gravitacional. No entanto, como o Sol possui massa muito superior à massa dos planetas que o orbitam, de modo que o centro de massa do sistema está praticamente situado nele, as leis de Kepler podem ser aplicadas à descrição do movimento planetário com grande precisão. Ademais, mesmo em situações em que não se aplicam de forma muito precisa, como no sistema Terra-Lua ou no caso dos satélites mais distantes do Sistema Solar, as leis de Kepler podem ser usadas como uma boa primeira aproximação para a descrição física do movimento.
Leia também:
Referências:
HEWITT, P. G. Conceptual Physics. 10. ed. San Francisco: Pearson, 2006. p. 199-200.
KEPLER, S. O.; SARAIVA, M. F. O. Astronomia & Astrofísica. São Paulo: Editora Livraria da Física, 2014. p. 80-81.
PIRES, A. S. T. Evolução das ideias da Física. 2. ed. São Paulo: Editora Livraria da Física, 2008. p. 102-111.
ROY, A. E.; CLARKE, D. Astronomy: Principles and Practice. 4. ed. Philadelphia: IoP, 2003. p. 170.