Para que Mendel pudesse chegar aos seus resultados, ele utilizou muitos métodos estatísticos para sua interpretação, calculando as probabilidades de ocorrer os eventos. A probabilidade serve para estimar matematicamente a possibilidade de ocorrer eventos que acontecem ao acaso, ou seja, por questão de sorte. Pode ser definida pela seguinte fórmula:
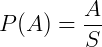
Onde P é a probabilidade de um evento ocorrer, A é o número de eventos desejados e S é o número total de eventos possíveis.
Exemplo: Quando jogamos uma moeda para cima, temos duas possibilidades de resultado: ela cair com a face “cara” voltada para cima, ou com a face “coroa” voltada para cima. Portanto temos duas possibilidades. A possibilidade de sair cara é de 1/2 ou 50%, pois temos uma chance (sair cara) em duas possibilidades (cara ou coroa).

assim como

A probabilidade é um evento esperado, uma possibilidade, portanto, não é certeza que vá ocorrer. Quanto mais repetições ocorrerem, mais chances a previsões terão de dar certo.
Quando utilizamos cálculos de probabilidades em genética, não podemos dizer que os indivíduos que irão nascer terão obrigatoriamente os genótipos calculados, pois é questão de sorte. Quanto mais indivíduos nascerem, mais chances dos resultados práticos se aproximarem dos cálculos.
Regra do “e”
Quando a ocorrência de um evento não afeta a ocorrência do evento seguinte, dizemos que eles são independentes. Quando queremos calcular a probabilidade da ocorrência de eventos independentes de uma vez só, utilizamos a regra do “e”.
Exemplo: Se jogarmos duas moedas para cima, qual a probabilidade de sair “cara” nas duas?
Resolução:
O fato de sair “cara” em uma moeda não afeta a chance de sair “cara” na outra. Quando acontece esse tipo de evento, multiplicamos as probabilidades dos eventos independentes:

R = 1/4 ou 25%
Em genética utilizamos a mesma linha de raciocínio. Por exemplo: Qual a probabilidade de um casal ter dois filhos do sexo feminino?
Resolução: O nascimento da primeira filha não afeta a chance de o segundo filho ser do sexo feminino, pois a segregação dos alelos de um gene é tão ao acaso quanto jogar uma moeda para cima e obter “cara” ou “coroa”. Portanto:

R = 1/4 ou 25%
Regra do “ou”
A regra do “ou” é utilizada quando queremos calcular a probabilidade de ocorrer um evento ou outro numa mesma oportunidade.
Por exemplo: Qual a chance de sair “cara” ou “coroa” em uma jogada de moeda?
Resolução: Esses dois eventos não ocorrem juntos, pois é um ou o outro, logo são mutuamente exclusivos. Quando temos esse tipo de situação, somamos as duas probabilidades:

R = 1
Exemplo 2:
Qual a probabilidade de um casal ter dois filhos, sendo um menino e uma menina?
Resolução: Para responder esta questão, utilizaremos as duas regras:
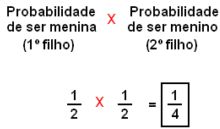 |
OU | 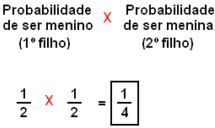 |

R = 1/2
Fontes
Amabis, José Mariano. Biologia. Volume 3. Editora Moderna.
Lopes, Sônia. BIO. Volume Único. Editora Saraiva
Texto originalmente publicado em https://www.infoescola.com/genetica/nocoes-de-probabilidade-em-genetica/