Como surgiu?
Todas as ideias matemáticas relacionam-se entre si, num dado momento ou em outro, porém o fato é que existe uma relação explícita ou implícita entre elas. Foi dessa forma, que o matemático e filósofo francês René Descartes concebeu a geometria analítica. Como à época álgebra e geometria eram cartas do mesmo baralho, mas tratadas como disjuntas, Descartes se dedicou a união dessas duas áreas do conhecimento matemático, para ele claramente correlacionáveis.
Pierre de Fermat (1901-1665)
Em seu livro, o discurso do método, publicado em 1637, Descartes mostra que as ciências deveriam ser guiadas pela matemática, isso devido a sua exatidão e possibilidades de experimentação. Foi nesse mesmo livro que René demonstrou o grande campo de aplicabilidades da geometria analítica. Porém, as indicações sobre quem possivelmente seria o patrono da G.A. (Geometria Analítica) não formam um senso comum. Muitos historiadores dão crédito também ao matemático Pierre de Fermat, vistos os seus estudos no campo das equações que representavam curvas no plano. Além disso, outros estudiosos apontam esse conhecimento como advindo, ora dos egípcios, ora dos gregos ou romanos.
O que é Geometria Analítica?
A geometria analítica, como discutido anteriormente, veio do ideal de unir álgebra e geometria. Num plano coordenado, podem ser localizadas retas, curvas, círculos, ou seja, todos os conceitos fundamentados na ideia primitiva de ponto, afinal todas essas figuras nada mais são que conjuntos de pontos.
Plano Cartesiano
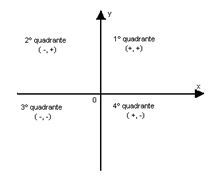
O plano coordenado, mais conhecido como Plano Cartesiano, é formado por dois eixos, um vertical, eixo y (eixo das ordenadas) e um horizontal, eixo x (eixo das abcissas), que formam quatro quadrantes, como mostra a figura ao lado. Esses dois eixos se coincidem num ponto comum chamado origem do plano, ou ponto (0,0). Um ponto é, desta forma, representado por dois valores numéricos, sendo que o primeiro corresponde a x e o segundo a y – (x,y) –. Esse par, ou par ordenado, ou ainda coordenadas cartesianas, no plano, indica um ponto.
Perceba que, a partir da álgebra, poderemos chegar a uma representação geométrica no plano, e vice-versa. No Plano de Descartes estão localizadas as definições matemáticas, antes apenas embutidas na geometria euclidiana (plana). Vejam na figura a seguir a representação de pontos no plano e entenda como ele funciona.
A (3,3) → (x,y)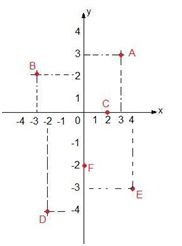
B (-3,2) → (x,y)
C (2,0) → (x,y)
D (-2,-4) → (x,y)
E (4,-3) → (x,y)
F (0, -2) → (x,y)
Onde usá-la ou encontrá-la?
A geometria analítica é a base de grandes campos de estudos matemáticos em dias atuais, mas também é muito utilizadas em atividades não explicitamente matemáticas. Seja na geometria algébrica, física, geometria diferencial, engenharia e outras, ou ainda na vida prática como nos mapas, satélites e no moderno Sistema de Posicionamento Global, GPS (sigla em inglês) ela está presente.
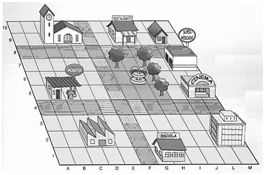Podemos utilizar o sistema de coordenadas para nos localizar, localizar pessoas ou imóveis, tendo por referência um ponto de origem (no qual estamos no momento), os eixos (ruas, avenidas, etc.) e um ponto de chegada (local no qual queremos chegar), como ilustra a imagem ao lado.
EXEMPLOS:
- Igreja (D, 9)
- Cinema (L, 5)
Para finalizar
Não importa quem foi o criador da geometria analítica, embora todos os seus contribuintes tenham muito mérito e mereçam a nossa admiração, gratidão e respeito, o importante é que essa descoberta revolucionou as nossas vidas, tornando-as mais práticas, convenientes e esclarecidas. Saber se deslocar num determinar espaço, mesmo que ele ainda lhe seja desconhecido, nos permite conhecer novos mundos, novos campos de conhecimentos, de conquistas, de descobertas.
A geometria analítica guia os nossos passos a cada instante das nossas vidas. Em momentos ela é útil aos profissionais da matemática, da física, da engenharia, etc. Em outros ela favorece aqueles que utilizam a matemática ou outras ciências inconscientemente, os leigos dos aspectos técnicos, porém essenciais ao funcionamento do mundo.
“A cada ponto, uma localização; a cada localização, um mundo que se revela”.
Por: Robison Sá.
Referências bibliográficas:
SOUZA, JOAMIR ROBERTO DE. Novo Olhar Matemática. – 1. ed. – São Paulo: FTD, 2010. – (Coleção novo olhar); v. 3)
____. Plano Cartesiano. Disponível em: http://cnsr103.blogspot.com.br/2010/05/grupo-6.html.
____. Plano Cartesiano. Disponível em: http://www.veragui.com.br/oitava/1_trimestre/2_trimestre/Revisao2/plano_cartesiano.htm.
E-BIOGRAFIAS. René Descartes. Disponível em: http://www.e-biografias.net/rene_descartes/.
Artigos de Geometria Analítica
Veja também: