Polígonos - Matemática e Geometria

Polígonos são figuras geométricas planas que são formadas por segmentos de reta a partir de uma sequência de pontos de um plano, todos distintos e não colineares, onde cada extremidade de qualquer um desses segmentos é comum a apenas um outro.

Eles podem ser côncavos ou convexos. Dados dois pontos A e B, interiores ao polígono, ele será convexo se, e somente se, o segmento de reta 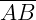$\overline{AB}$ estiver contido inteiramente no polígono. Caso contrário, ele será côncavo.

Polígono convexo. A reta 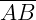$\overline{AB}$ está inteiramente contida no polígono.

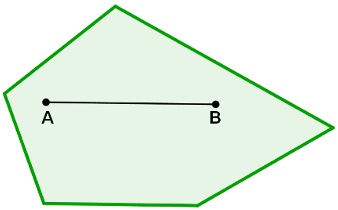
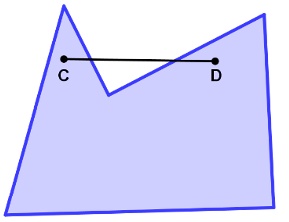
Polígono côncavo ou não convexo. A reta 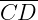$\overline{CD}$ não está inteiramente contida no polígono.

Polígonos simples

Dizemos que um polígono é simples quando quaisquer dois lados não consecutivos não se interceptam. Quando o polígono não é simples, dizemos que ele é complexo.

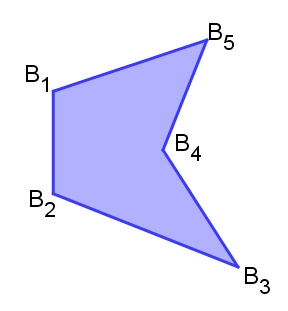Os polígonos A₁A₂A₃A₄A₅ e B₁B₂B₃B₄B₅ são polígonos simples.

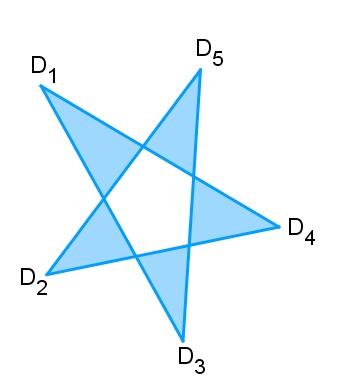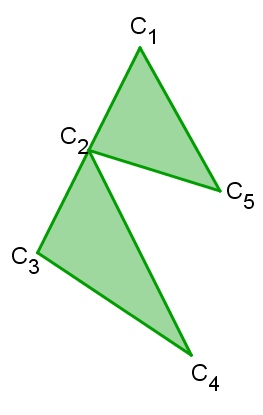
Os polígonos C₁C₂C₃C₄C₅ e D₁D₂D₃D₄D₅ são polígonos complexos.

Polígonos Regulares e Irregulares

Um polígono que possui os lados congruentes é chamado de equilátero. Quando possui os ângulos congruentes, é chamado de equiângulo.

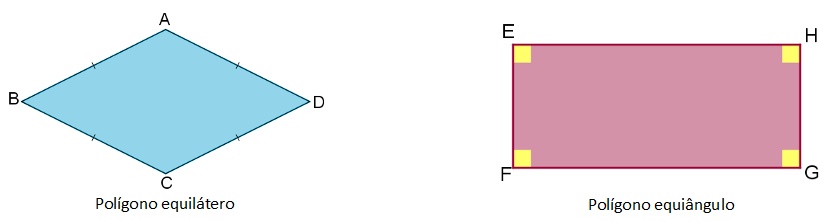
Um polígono convexo é regular se for equilátero e equiângulo, ou seja, quando seus lados são todos iguais (possuem a mesma medida) e seus ângulos internos também são iguais.

Nome dos polígonos

Podemos dar nomes aos polígonos de acordo com a quantidade de lados que ele possui. Abaixo, uma tabela apresentando o nome de cada polígono considerando seus lados.

# de Lados	Nome
3	Triângulo ou trilátero
4	Quadrângulo ou quadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octógono
9	Eneágono
10	Decágono
11	Hendecágono ou Undecágono
12	Dodecágono
15	Pentadecágono
20	Icoságono
n	n-látero

Geralmente, para polígonos com lados maiores que 20, nos referimos a ele apenas explicitando o seu número de lados. Por exemplo, um polígono de 27 lados.