Adição e subtração de Matrizes - Matemática

Ouça este artigo:

Por Robison Sá

Neste trabalho, o leitor irá encontrar conceitos e aplicações referentes às operações de adição e subtração de matrizes, sob a ótica da Educação Matemática, procurando apontar o desenvolvimento dos conceitos, mas também mostrando os atalhos nas resoluções de problemas e cálculos matemáticos encontrados no cotidiano do caro estudante.

O desenvolvimento das matrizes – como conhecemos em dias atuais – foi dado no século XX. Os principais nomes deste campo são os matemáticos Augustin Cauchy (1789-1857), que apresentou um trabalho baseado nas tabelas de números divulgadas no século XVIII, e J. Jacobi (1804-1851), Arthur Cayley e Francesco Brioschi (1824-1897), que também apresentaram trabalhos importantes alicerçados no trabalho de Cauchy.

Mesmo antes do século XX, precisamente no século XVIII, Leibniz e Seki, na Alemanha e no Japão respectivamente, já tinham desenvolvido métodos de resolução de problemas envolvendo sistemas lineares utilizando tabelas numéricas semelhantes às matrizes modernas. Ainda durante o século XVIII outros matemáticos apresentaram seus trabalhos à comunidade científica: Pierre Laplace (1749-1827) e Alexandre Vandermonde (1735-1796) são exemplos deles.

Adição de matrizes

Partindo de duas matrizes A e B de mesmo tipo, ou seja, A = (a_ij)_mxn e B = (b_ij)_mxn, podemos encontrar a matriz soma (A + B), bastando, para isso, somarmos os elementos correspondentes de A e B.

Exemplo 1

Dadas as matrizes , determinar a matriz soma (A + B).

Como A = (a_ij)_2x2 e B (b_ij)_2x2, isto é, A e B têm o mesmo tipo, podemos somar os termos correspondentes para encontrarmos a matriz soma(A + B)_2x2.

Propriedades da adição

Sendo A, B, C e O (matriz nula) matrizes de mesmo tipo e p, q Î, valem as propriedades:

Comutativa: A + B = B + A
Associativa: A + (B + C) = (A + B) + C
Elemento Neutro: A + O = O + A = A

(Youssef et al., 2005)

Matriz oposta

Dada uma matriz (A), sua oposta (–A) é aquela que adicionada a A resulta uma matriz nula (aquela na qual os elementos são iguais à zero).

Em geral, temos...

Perceba que, nas matrizes A e - A, os elementos correspondentes são opostos.

Exemplo 2

Vamos tomar como exemplo a matriz , a oposta de A será .

Acompanhe:

Subtração de Matrizes

Partindo de duas matrizes (A e B) de mesmo tipo, ou seja, A = (a_ij)_mxn e B = (b_ij)_mxn, podemos encontrar a matriz diferença (A – B) subtraindo os seus elementos correspondentes entre si.

Exemplo 3

Determine a matriz diferença entre .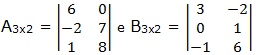

Vamos procurar a matriz diferença (A – B)_3x2...

“Adicionemos as ações boas e subtraiamos as ruins.”

(Robison Sá)

Referências bibliográficas:
SOUZA, Joamir Roberto de. Novo Olhar Matemática. – 1 ed. – São Paulo: FTD, 2010. – (Coleção novo olhar; v. 2)
YOUSSEF, Antonio Nicolau. Matemática: ensino médio, volume único / Antonio Nicolau Youssef, Elizabeth Soares, Vicente Paz Fernandez. – São Paulo: Scipione, 2005.

Texto originalmente publicado em https://www.infoescola.com/matematica/adicao-e-subtracao-de-matrizes/