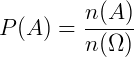O Exame Nacional do Ensino Médio (Enem) foi criado pelo Ministério da Educação, inicialmente, para verificar o desempenho dos alunos brasileiros ao final do terceiro ano do ensino médio, portanto, no encerramento da educação básica. Hoje, o Enem é adotado nas Universidades Públicas e em grande parte das privadas como forma de ingresso na carreira acadêmica em substituição do antigo vestibular.
Gostaria de deixar claro, que as possibilidades de resolução das questões demonstradas neste trabalho não encerra o número de maneiras pelas quais o candidato poderá chegar à resposta correta desses problemas, apenas faço um comparativo entre o “como o candidato geralmente resolve o problema” e “como ele seria mais rapidamente resolvido”. A minha intenção é favorecer o tempo de resolução das questões, contribuindo para o êxito do candidato no Exame.
Conteúdo deste artigo
Questões comentadas
O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há:
- 10 alunos a mais do que possíveis respostas distintas.
- 20 alunos a mais do que possíveis respostas distintas.
- 119 alunos a mais do que possíveis respostas distintas.
- 260 alunos a mais do que possíveis respostas distintas.
- 270 alunos a mais do que possíveis respostas distintas.
(Enem 2012, 2º dia, Caderno 5 – Amarelo – Página 19, Matemática e Suas Tecnologias, Questão 136)
Comentários e Solução
Os leitores deste trabalho, que já experimentaram o Enem, sabem que as questões são longas, ou seja, um texto que exige do candidato um bom nível de interpretação e raciocínio nos desenvolvimentos posteriores. Na questão acima, para aquele candidato que não possui o embasamento matemático para ir direto a sua solução, pode-se cometer vários equívocos e a perda de tempo que, possivelmente, implicará em seu fracasso.
- Primeira Possibilidade: o candidato desatento, ao chegar à leitura da última opção, já não lembrará mais o que a questão solicita em sua solução, portanto leia o enunciado atentamente, releia-o se for necessário, para que ao final você possa compreender o que realmente pede a questão.
- Segunda Possibilidade: o candidato poderá, erroneamente, tentar encontrar, ao invés do número de possibilidades na distribuição dos objetos feita pelos personagens pelos cômodos da casa, qual personagem escondeu determinado objeto e em qual local, visto que o enunciado propõe isso, mas a pergunta não. Isso com certeza o levará a perda de tempo desnecessária e a frustração de não encontrar as respostas que o exame solicita.
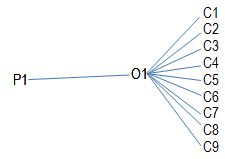
- Terceira Possibilidade: o candidato tentará formar uma árvore de possibilidades do tipo mostrado abaixo, o que não é errado, mas demanda muito tempo e, no Enem, o relógio não conspira a favor do candidato, muito pelo contrário. Veja!Representando o personagem 1 por P1, o objeto 1 por O1 e os cômodos respectivamente por C1, C2, C3, C4, C5, C6, C7, C8 e C9, formaremos uma árvore de possibilidades restrita a apenas um personagem – neste exemplo.
Daí se formaria uma nova árvore, ainda para o primeiro personagem, desta vez para o objeto 2. Depois uma outra para o mesmo personagem e para o objeto 3, e assim sucessivamente. Ainda poderiam ser ramificadas, nesta mesma árvore, as possibilidades para os objetos 2, 3, 4 e 5.Para o primeiro objeto, o personagem 1 terá nove possibilidades de distribuição pelos cômodos da casa. Como há 5 objetos, multiplicaremos 5 (objetos) x 9 (possibilidades de distribuição) e obteremos 45 possibilidades distintas somente para o primeiro personagem. Perceba que através deste método chega-se ao resultado esperado, isto é, 45 possibilidades para o primeiro personagem multiplicado pelo número de personagens (6), 45 x 6 = 270. Como temos 280 participantes nessa brincadeira, subtraindo 270 desse total obteremos 10, ou seja, 10 alunos a mais do que possíveis respostas distintas, ALTERNATIVA (A). Porém, este método demanda muito tempo; por isso aconselho o método posterior. - Quarta Possibilidade: Acertadamente, o candidato deverá buscará seguir o Princípio Fundamental da Contagem. Acompanhem: 5 objetos, 6 personagens e 9 cômodos. Basta que multipliquemos esses valores entre si: 5 x 6 x 9 = 270. Como temos 280 participantes nessa brincadeira, subtraindo 270 desse total obteremos 10, ou seja, 10 alunos a mais do que possíveis respostas distintas, ALTERNATIVA (A).Para fim de clareza veja a definição formal do Princípio Fundamental da Contagem.“Se um acontecimento A pode ocorrer de n maneira distintas e, para cada uma dessas maneiras, um acontecimento B pode ocorrer de m maneiras distintas, então a quantidade de possibilidades de ocorrência dos acontecimentos A e B é dada pelo produto n.m. Este princípio, chamado princípio fundamental da contagem, é válido para qualquer número de acontecimentos.” (SOUZA, 2010, p.217) [grifos meus]
Em um jogo há duas urnas com 10 bolas de mesmo tamanho em cada urna. A tabela a seguir indica as quantidades de bolas de cada cor em cada urna.
Cor
Urna 1
Urna 2
Amarela
4
0
Azul
3
1
Branca
2
2
Verde
1
3
Vermelha
0
4
Uma jogada consiste em:
- o jogador apresenta um palpite sobre a cor da bola que será retirada por ele da urna 2;
- ele retira, aleatoriamente, uma bola da urna 1 e a coloca na urna 2, misturando-a com as que lá estão;
- em seguida ele retira, também aleatoriamente, uma bola da urna 2;
- se a cor da última bola retirada for a mesma do palpite inicial, ele ganha o jogo.
Qual cor deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar?
- Azul.
- Amarela.
- Branca.
- Verde.
- Vermelha.
(Enem 2012, 2º dia, Caderno 5 – Amarelo – Página 19, Matemática e Suas Tecnologias, Questão 138)
Comentários e Solução
Essa questão, assim como quase todas, relacionadas à matemática, poderá ser resolvida de muitas maneiras, utilizando vários segmentos lógicos ou ferramentas matemáticas; a diferença é o ganho de tempo que deve ser considerado no Enem. Veja abaixo, que podemos ir por caminhos complexos, enfadonhos e longos ou partir para uma resposta prática e objetiva, embasada no raciocínio lógico, na observação acurada.
|
Cor |
Urna 1 |
Urna 2 |
|
Amarela |
4 |
0 |
|
Azul |
3 |
1 |
|
Branca |
2 |
2 |
|
Verde |
1 |
3 |
|
Vermelha |
0 |
4 |
Primeira Possibilidade: O candidato poderá ir para o caminho do cálculo das probabilidades de retirada de cada cor pelo jogador da urna 1, depois da urna 2, passar uma bola da urna 1 para a urna 2 e depois ver qual a maior chance de retirada de determina cor, como veremos a seguir.
Como as urnas 1 e 2 têm 10 bolas cada uma (casos possíveis), pode-se dividir a quantidade de bolas correspondente a cada cor (número de casos favoráveis) pelo número total de bolas da urna.
Antes de prosseguir, quero registrar aqui a definição matemática que embasa a minha colocação.
“Considere um evento A de um espaço amostral W finito e equiprovável. A razão entre a quantidade de elementos de A (indicada por n(A)) e a quantidade de elementos de W (indicada por n(W)) é a probabilidade P(A) de o evento A ocorrer.”
(SOUZA, 2010, P.253)
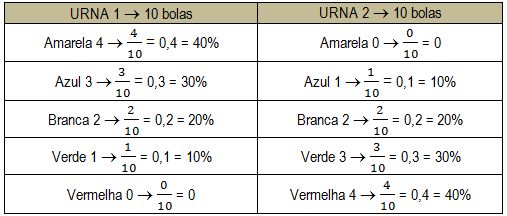
Agora vamos prosseguir, uma vez que sabemos o número de bolas correspondente a cada cor, podemos encontrar a probabilidade de retirada delas pelo jogador.
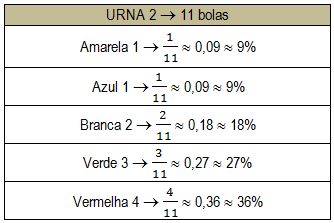
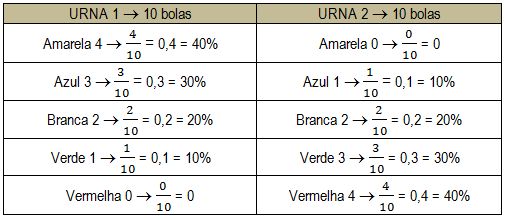
O enunciado diz que o jogador, após arriscar um palpite, retira uma bola da urna 1 e a coloca na urna 2, misturando-a junto as outras. Olhando a urna 1, visivelmente percebemos que a maior chance é de ser retirada uma bola amarela, visto que a ela corresponde 40% das possibilidades. Ao transportar essa bola amarela para a urna 2, teríamos novas probabilidades para ela, pois o número de bolas total foi alterado, de 10 para 11, assim como ocorreu um acréscimo de uma bola relativo a cor amarela. Vejamos como fica a urna 2 após receber mais uma bola amarela.
A partir da análise da tabela acima, podemos afirmar que a cor que deve ser escolhida pelo jogador para que ele tenha a maior probabilidade de ganhar é a cor VERMELHA, ALTERNATIVA E.
Segunda Possibilidade: aqui, para poupar tempo, eu mostro que seria possível ao candidato encontrar a resposta desejada sem a ajuda dos cálculos probabilísticos, pelo menos explícitos. Podemos utilizar apenas o raciocínio para deduzir a resposta procurada.
Veja que temos mais bolas amarelas na urna 1, portanto teremos mais chances de retirá-las primeiramente. Ao transportar uma dessas bolas amarelas para a urna 2, ficaremos com apenas 1 bola amarela nesta urna. Sendo assim, como temos 4 bolas vermelhas na urna 2 (maior número de bolas que as outras), podemos concluir que há maiores chances de acerto se o jogador escolher a cor VERMELHA, ALTERNATIVA E.
Considerações finais
Como afirmei na introdução deste trabalho, descrevo aqui alguns caminhos pelos quais, se o candidato seguir, poupará tempo, chegando mais rapidamente à resposta desejada na questão. Lembrem-se de que o conhecimento das ferramentas matemáticas é primordial para o sucesso no Enem, mas não só ele é o responsável por este sucesso, este deve ser aliado à boa interpretação, a atenção, ao raciocínio e aos atalhos – caminhos pelos quais chegaremos à mesma solução com economia de tempo.
Este artigo faz parte de uma série de artigos que serão publicados neste espaço com vista à melhora do desempenho do candidato no Enem, dando-lhes suporte, oferecendo-lhe dicas importantes na resolução de questões do Exame, analisando detalhadamente as suas questões, ou seja, ofertando ao futuro candidato todo um aparato de ferramentas matemáticas e não matemáticas, que o ajudará a lograr êxito e ingressar na carreira acadêmica.
“O sucesso é possível àqueles que se dedicam a encontrá-lo.” (Robison Sá)
Referências bibliográficas
SOUZA, JOAMIR ROBERTO DE. Novo olhar matemática. – 1 ed. – São Paulo: FTD, 2010.
GIOVANNI, JOSÉ RUY; BONJORNO, JOSÉ ROBERTO. Matemática 2: progressões, matrizes, análise combinatória e geometria: 2° grau. São Paulo: FTD, 1992.
INEP. Provas e Gabaritos. Disponível em: http://inep.gov.br/web/enem/edicoes-anteriores/provas-e-gabaritos. Acesso em: 02 de julho de 2013.
Texto originalmente publicado em https://www.infoescola.com/matematica/analise-de-questoes-de-matematica-do-enem/