Área de polígonos irregulares

Polígonos irregulares

Polígonos são figuras geométricas planas que são formadas por segmentos de reta a partir de uma sequência de pontos de um plano, todos distintos e não colineares, onde cada extremidade de qualquer um desses segmentos é comum a apenas um outro.

Um polígono é irregular quando seus lados não são todos iguais e seus ângulos internos não tem a mesma medida.

Na geometria plana, existem diferentes tipos de polígonos irregulares. Para muitos deles, há uma fórmula matemática para se calcular sua área; outros requerem um método diferente.

Área de um retângulo

Um retângulo é um polígono irregular, pois seus lados são dois a dois diferentes, ou seja, o valor da medida da base é sempre diferente do valor da medida da altura.

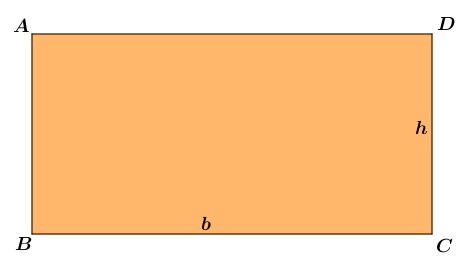
A área desse polígono irregular pode ser calculada multiplicando-se a sua base pela sua altura.

$A = \text{base } \times \text{ altura} = b \cdot h$

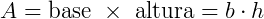
Área de um triângulo irregular

Sabemos que existem três tipos de triângulos: escaleno (seus três lados são diferentes), isósceles (dois lados iguais e um diferente) e equilátero (seus três lados são iguais). Somente dois deles são irregulares: escaleno e isósceles. O triângulo equilátero, por possuir seus três lados iguais, é dito como regular.

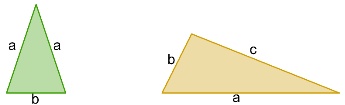
Para calcular a área desses polígonos irregulares, utilizamos a fórmula:

$A = \frac{\text{base } \times \text{ altura}}{2} = \frac{b \cdot h}{2}$

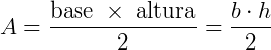
Área de um trapézio

Trapézios são polígonos quadriláteros que apresentam dois de seus lados paralelos, que são chamados de base maior e base menor. Eles são classificados em trapézio retângulo (possui dois ângulos de 90°), trapézio isósceles (além de seus lados paralelos, os outros dois são congruentes) e trapézio escaleno (todas as medidas são diferentes).

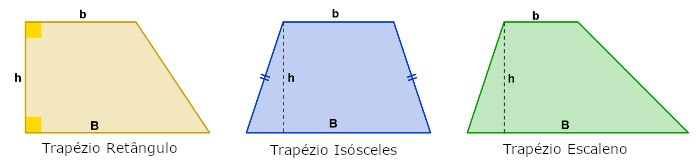
A área de um trapézio é calculada através da fórmula:

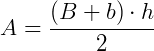
Onde b é a base menor, B é a base maior e h é a altura.

Área de um paralelogramo

O paralelogramo é um quadrilátero (polígono de quatro lados) cujo seus lados opostos são paralelos.

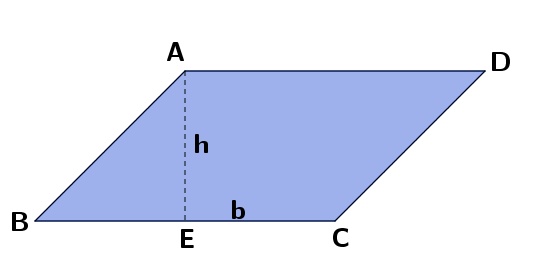
A área de um paralelogramo pode ser calculada multiplicando- se a sua base pela sua altura.

$A = \text{base } \times \text{ altura} = b \cdot h$

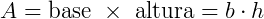
Onde b (base) é a medida de qualquer um dos lados e h é a altura relativa a esse lado.

Área de um losango

O losango é um quadrilátero (polígono de quatro lados) cuja medida de seus lados são iguais. Além disso, possui dois ângulos opostos obtusos (maiores que 90°) outros dois ângulos opostos agudos (menores que 90°).

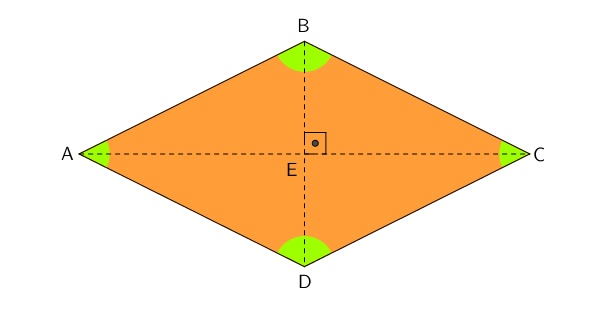
Uma das maneiras de calcular a área de um losango é multiplicando-se as suas diagonais e dividindo o resultado obtido pela metade, veja:

$A = \frac{D \cdot d}{2}$

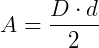
Onde D é a medida da diagonal maior (AC) e d a medida da diagonal menor (BD).

Área de polígonos irregulares diversos

Vimos acima fórmulas para calcular a área de alguns polígonos irregulares mais conhecidos. Agora, veremos como calcular a área de um polígono irregular qualquer, como o seguinte:

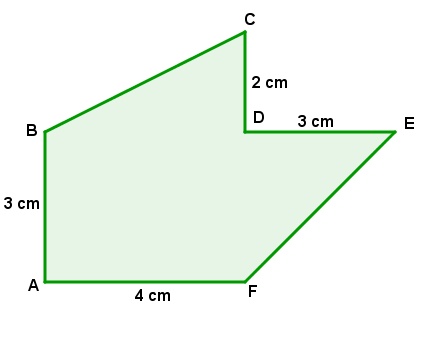Uma maneira bastante simples para calcular a área deste polígono, é dividir este polígono em outros cuja área é fácil de se calcular ou a fórmula da área é conhecida. Vamos dividi-lo da seguinte maneira.

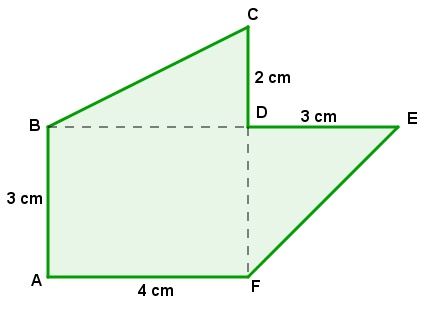
Conseguimos dividir o polígono em três outros: um retângulo e dois triângulos.

A área do polígono ABCDEF será a soma das áreas desses três outros polígonos, ou seja:

$A_\text{ABCDEF} = A_\text{ABDF} + A_\text{BCD} + A_\text{DEF}$

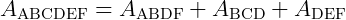
Vamos, então, calcular cada uma das áreas:

A área do retângulo ABDF será:

$A_\text{ABDF} = 4 \cdot 3 = 12cm^2$

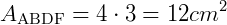
No triângulo BCD, a altura será o lado DC = 2 cm e a base será o lado BD, que tem a mesma medida que o lado AF, assim, BD = 4 cm.

$A_\text{BCD} = \frac{\text{base } \times \text{ altura}}{2} = \frac{4 \cdot 2}{2} = \frac{8}{2} = 4cm^2$

No triângulo DEF, a base será o lado DE = 3 cm e a altura será o lado DF, que tem a mesma medida que o lado AB, assim, DF = 3 cm.

$A_\text{DEF} = \frac{\text{base } \times \text{ altura}}{2} = \frac{3 \cdot 3}{2} = \frac{9}{2} = 4,5cm^2$

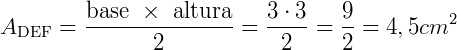
Assim, a área total do polígono ABCDEF será:

$A_\text{ABCDEF} = 12 + 4 + 4,5= 20,5cm^2$

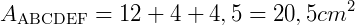
Exemplo:

Calcular a área do polígono irregular ABCD a seguir:

$\Downarrow$

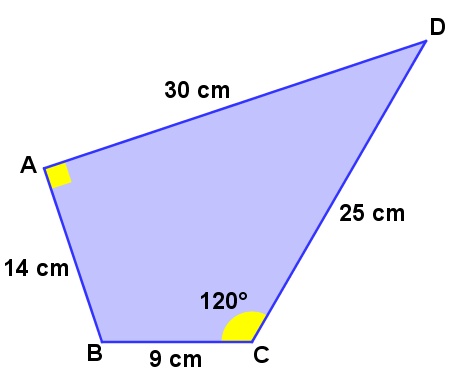
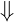
Veja que dividimos ABCD em dois triângulos: ABD e BCD.

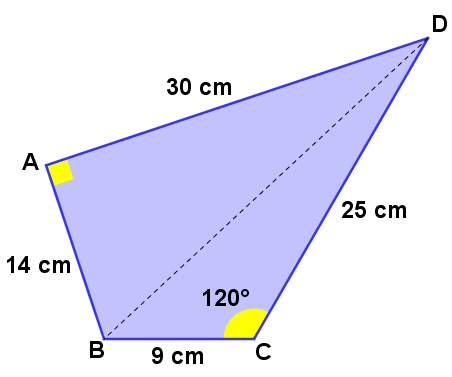
Vamos calcular a área de ABD.

Temos que a base será AB = 14 cm e a altura será AD = 30 cm. Observe que, nesse caso AD será a altura porque o triângulo ABD é retângulo e nos triângulos retângulos, um cateto sempre será a altura relativa ao outro cateto.

$A_\text{ABD} = \frac{\text{base } \times \text{ altura}}{2} = \frac{14 \cdot 30}{2} = \frac{420}{2} = 210cm^2$

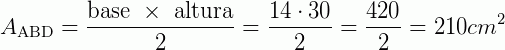
Para calcular a área do triângulo BCD, precisamos da sua altura. Mas como o ângulo entre dois lados conhecidos já foi dado, podemos usar a fórmula 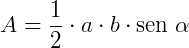$A = \frac{1}{2} \cdot a \cdot b \cdot \text{sen }\alpha$, onde a e b são os lados desse triângulo e 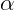$\alpha$ é a medida do ângulo dado.

$A = \frac{1}{2} \cdot 9 \cdot 25 \cdot sen(120^o)$

$A = \frac{1}{2} \cdot 225 \cdot sen(60^o)$

$A = \frac{225}{2} \cdot \frac{\sqrt{3}}{2}$

$A = \frac{225 \sqrt{3}}{4} = 97,4 cm^2$

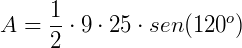
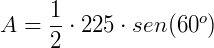
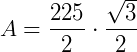
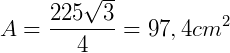
Agora, vamos somar a área dos dois triângulos e determinar a área do polígono ABCD:

$A_\text{ABCD} = 210 + 97,4 = 307,4cm^2$

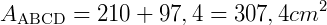
Referências:

DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.

DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.

RIBEIRO, Paulo Vinícius. Matemática: Teorema de Tales e quadriláteros. Vol. 4. São Paulo: Bernoulli.

Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-poligonos-irregulares/