Área de quadrados e retângulos - Geometria - Matemática

Quadrados e retângulos são quadriláteros (polígono de quatro lados).

O retângulo é definido como uma figura geométrica plana que possui os lados opostos paralelos entre si e seus ângulos internos são todos congruentes.

Um quadrado é um caso especial de retângulo. É um retângulo onde os seus lados têm sempre a mesma medida.

Tanto o retângulo quanto o quadrado, possuem 4 lados e, portanto, 4 ângulos com 90° cada.

No retângulo, os lados AB e CD são congruentes, assim como os lados AD e BC.

No quadrado, todos os lados são congruentes, ou seja, possuem a mesma medida.

Área de um quadrado ou retângulo

Área é o espaço interno de qualquer figura geométrica plana.

Tanto a área de um retângulo quanto a de um quadrado pode ser calculada multiplicando- se a sua base pela sua altura.

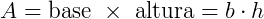
$A = \text{base } \times \text{ altura} = b \cdot h$

Onde b (base) é a medida de qualquer um dos lados e h é a altura relativa a esse lado.

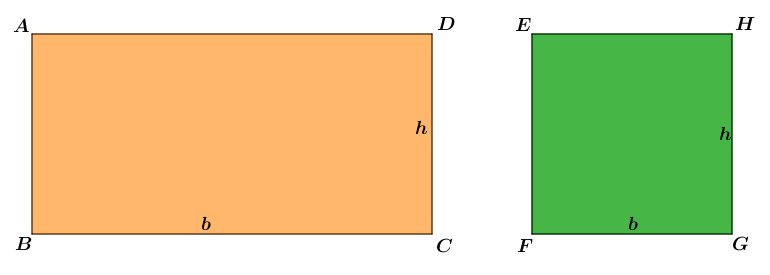
Podemos expressar a área do quadrado de uma outra maneira. Como ele possui 4 medidas iguais. Vamos chamar de a.

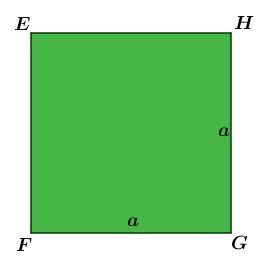
Aplicando a fórmula que vimos acima, teremos que a área será a base multiplicado pela altura:

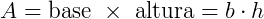
$A = \text{base } \times \text{ altura} = b \cdot h$

Acontece que o quadrado possui a mesma medida para a base e para a altura que chamamos de a. Assim:

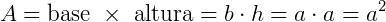
$A = \text{base } \times \text{ altura} = b \cdot h = a \cdot a = a^2$

Assim, para encontrar a área de um quadrado, basta elevar a medida de seu lado, ao quadrado.

$A = a^2$

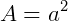
Exemplos:

Encontre a área de um quadrado de 20 m de lado:

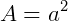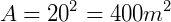
Como se trata de um quadrado e sabemos a medida do lado, podemos usar a fórmula $A = a^2$ .

$A = 20^2 = 400m^2$

Portanto, a área do quadrado será 400 m².

Qual a área de um retângulo que possui 8 cm de base e 10 cm de altura?

Como se trata de um retângulo, para encontrar a área, basta multiplicar a base pela sua altura:

$A = b \cdot h$

$A = 8 \cdot 10 = 80cm^2$

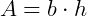
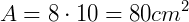
Portanto, a área do retângulo será 80 cm².

Imagine um quadrado com lado igual a 4 m.

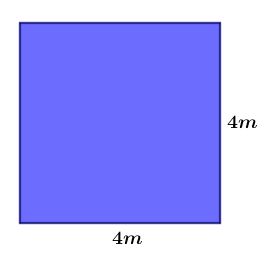
Sua área será:

$A = a^2$

$A = 4^2$

$A = 16m^2$

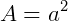
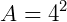
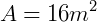
Encontrar a área, no caso em metros, significa dizer quantos quadradinhos menores, com 1 m de lado cabem desse quadrado maior.

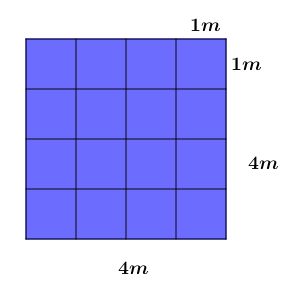Olhando a figura acima, podemos ver que há 16 quadradinhos menores, com lado igual a 1 m. Ou seja, 16 m², como havíamos calculado anteriormente.

Referências:
DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.

RIBEIRO, Paulo Vinícius. Matemática: Teorema de Tales e quadriláteros. Vol. 2. São Paulo: Bernoulli.