Área de um paralelogramo

O que é um paralelogramo?

O paralelogramo é um quadrilátero (polígono de quatro lados) cujo seus lados opostos são paralelos.

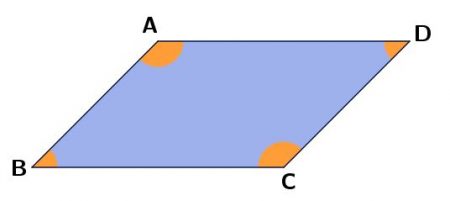
Os lados opostos AB e CD são paralelos e congruentes, assim como os lados AD e BC.

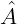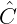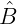Assim como os lados, os ângulos opostos também são congruentes, ou seja $\hat{A}$, é oposto a $\hat{C}$ e $\hat{B}$ é oposto a 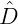$\hat{D}$. Então e são congruentes, assim como 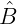$\hat{B}$ e $\hat{D}$.

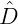Observe que todo quadrado, retângulo e losango também é um paralelogramo.

Área de um paralelogramo

Área é o espaço interno de qualquer figura geométrica plana.

A área de um paralelogramo pode ser calculada multiplicando- se a sua base pela sua altura.

$A = \text{base } \times \text{ altura} = b \cdot h$

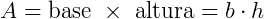
Onde b (base) é a medida de qualquer um dos lados e h é a altura relativa a esse lado.

Existe uma demonstração simples que mostra como obtemos esta fórmula.

Imagine um paralelogramo qualquer de base b e altura h:

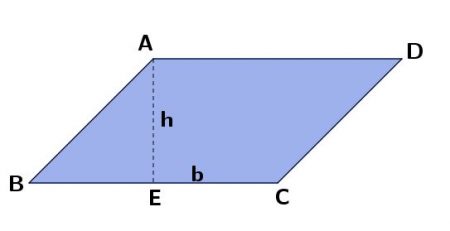Se deslocarmos o triângulo ABE para o lado direito, de forma que os lados AB e DC se unam, teremos um retângulo de base b e altura h.

Agora que obtemos um retângulo, podemos calcular sua área através da fórmula 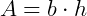$A = b \cdot h$

Assim, concluímos que a fórmula para calcular a área de um paralelogramo é a mesma que utilizamos para calcular a área de um retângulo: 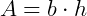$A = b \cdot h$

Exemplo:

Calcule a área de um paralelogramo com altura de 28 cm e base de 12 cm:

Temos que b = 12 cm e h =28 cm

Aplicando a fórmula: 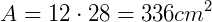$A = 12 \cdot 28 = 336 cm^2$

Existe outra maneira de calcular a área de um paralelogramo, apenas com as medidas de dois lados e do ângulo formado por esses lados.

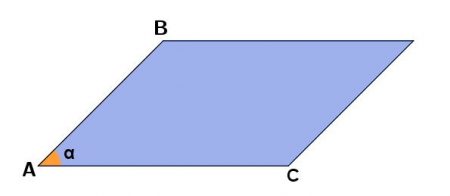Considerando as medidas dos lados AB e AC e o ângulo entre eles, podemos encontrar a área do paralelo gramo através da formula: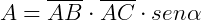 $A = \overline{AB} \cdot \overline{AC} \cdot sen\alpha$

Se chamarmos esses lados simplesmente de a e b, teremos: 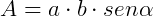$A = a \cdot b \cdot sen\alpha$

Exemplo:

Calcule a área de um paralelogramo em que dois lados consecutivos têm medidas de 6 cm e 10 cm respectivamente e formam um ângulo de 30°.

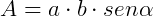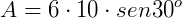
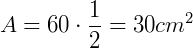
Como não temos o valor da altura, podemos utilizar a fórmula $A = a \cdot b \cdot sen\alpha$.

$A = 6 \cdot 10 \cdot sen30^o$

$A = 60 \cdot \frac{1}{2} = 30 cm^2$

Referências:

DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol. 9. São Paulo: Atual, 1995.

RIBEIRO, Paulo Vinícius. Matemática: Teorema de Tales e quadriláteros. Vol. 2. São Paulo: Bernoulli.

Texto originalmente publicado em https://www.infoescola.com/matematica/area-de-um-paralelogramo/