Dada uma sequência de pontos de um plano (A1, A2, ..., An) com n ≥ 3, todos distintos, onde três pontos consecutivos não são colineares, considerando-se consecutivos An-1, An, e A1, assim como An, A1 e A2, chama-se polígono à reunião dos segmentos A1A2, A2A3, A3A4, ... An-1An, AnA1.
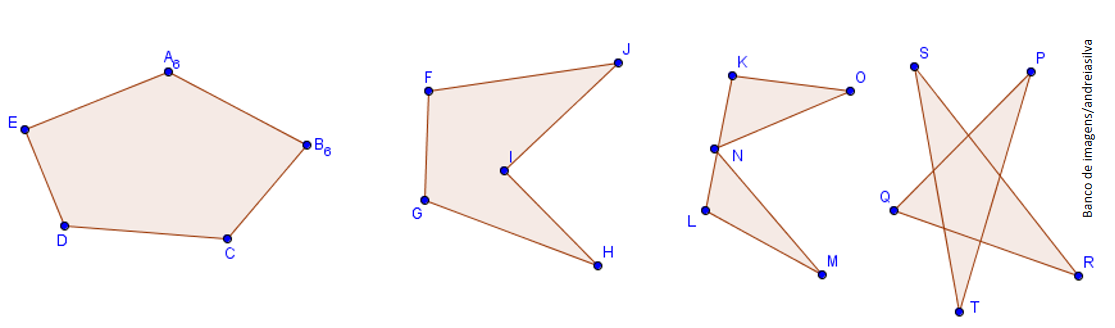
Considerando o polígono A1, A2, A3, ..., An, An-1, temos:
os pontos A1, A2, A3, ... , An-1, An são os vértices do polígono
os segmentos A1A2, A2A3, ... , An-1An, AnA1 são os lados do polígono; e os ângulos
Â1 = AnÂ1A2, Â2 = A1Â2A3, Ân = An-1ÂnA1
são os ângulos do polígono.
Dois lados que têm um vértice comum (ou uma extremidade comum) são lados consecutivos.
Dois lados não consecutivos não têm vértice (ou extremidade) comum.
Dois ângulos de um polígono são consecutivos se têm um lado do polígono comum.
Um polígono de n vértices possui n lados e n ângulos.
A soma dos lados é o perímetro do polígono.
Perímetro de A1 A2 A3 ... An-1 An = A1A2+ A2A3 + An-1An + AnA1
Conteúdo deste artigo
Polígono convexo e polígono côncavo
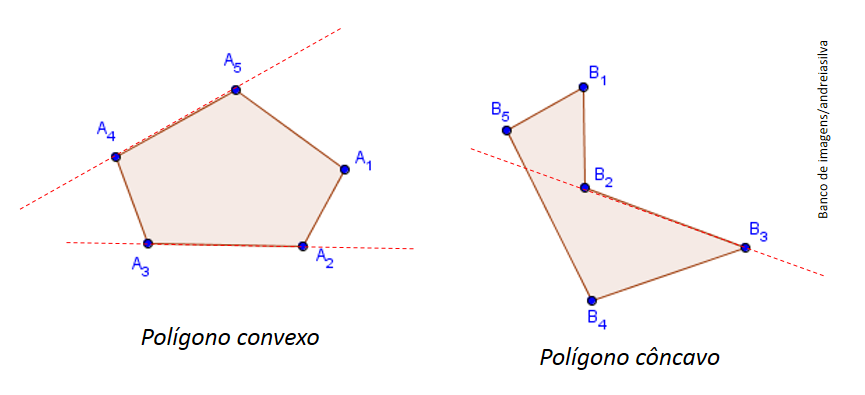
Um polígono é um polígono convexo se, e somente se, a reta determinada por dois vértices consecutivos quaisquer deixa todos os demais (n -2) vértices num mesmo plano dos dois que ela determina.
Se um polígono não é polígono convexo, dizemos que ele é um polígono côncavo.
Polígono regular
Um polígono que possui os lados congruentes é equilátero. Se possui os ângulos congruentes, é equiângulo.
Um polígono convexo é regular se, e somente se, tem todos os lados congruentes (é equilátero) e todos os ângulos congruentes (é equiângulo).
Nome dos polígonos
De acordo com o número n de lados, os polígonos recebem nomes especiais.
| Número de lados | Nome do polígono |
| 3 | triângulo |
| 4 | Quadrilátero |
| 5 | pentágono |
| 6 | hexágono |
| 7 | heptágono |
| 8 | octógono |
| 9 | eneágono |
| 10 | decágono |
| 11 | undecágono |
| 12 | dodecágono |
| 15 | pentadecágono |
| 20 | icoságono |
Perímetro de polígonos regulares
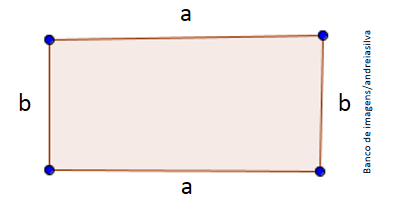
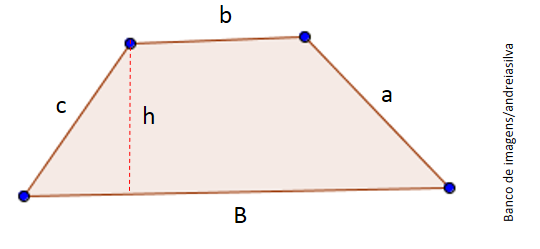
Perímetro = 2a + 2b
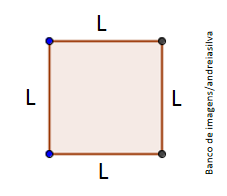
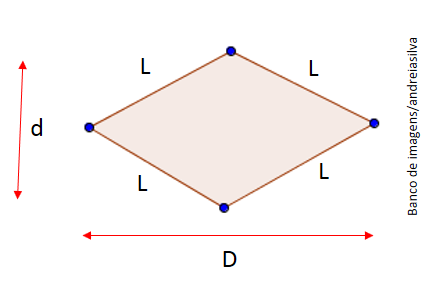
Perímetro = 4L
Medida da área de um polígono regular qualquer
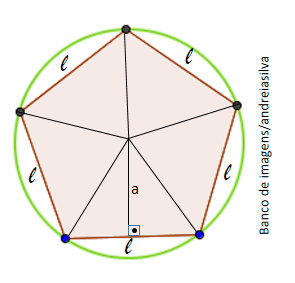
Um modo de obter a medida da área de um polígono regular é por meio de sua decomposição em triângulos congruentes. O pentágono regular, por exemplo, pode ser decomposto em 5 triângulos. Observe a figura abaixo.
Um polígono regular com um número n qualquer de lados pode ser decomposto em n triângulos congruentes.
A altura de cada um dos triângulos corresponde ao apótema de medida de comprimento a do polígono regular inscrito na circunferência. Portanto, a medida da área de cada um dos n triângulos é dada por 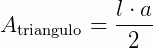 .
.
Assim, a medida da área total do polígono regular é:
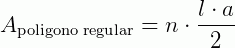
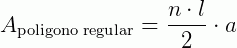
O semiperímetro é a medida da metade do perímetro. No caso de um polígono regular de n lados, o semiperímetro (p) é dado por:
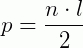
Assim , temos:
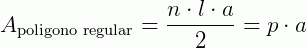
A medida da área de um polígono regular é igual ao produto do semiperímetro pela medida do apótema:
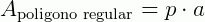
Referências bibliográficas:
1. A. Caminha. Tópicos de Matemática Elementar, Volume 2: Gemoetria Euclidiana Plan.Rio de Janeiro, SBM, 2013.
2. O. Dolce e J. N. Pompeo. Os Fundamentos da Matemática Elementar, Volume 9: Geometria Plana. São Paulo, Atual editora, 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/calculo-do-perimetro-e-area-de-poligonos/