Círculo trigonométrico

Chamamos de círculo trigonométrico (circunferência trigonométrica ou ciclo trigonométrico) a circunferência orientada, de centro na origem do sistema de coordenadas cartesianas ortogonais, cujo raio tem 1 unidade de comprimento e na qual o sentido positivo é o anti-horário.

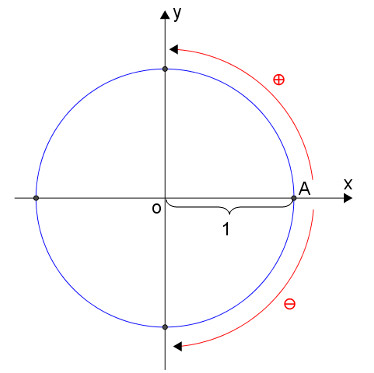
Todo círculo trigonométrico tem início no ponto A e gira sempre no sentido anti-horário, ou seja, sentido positivo.

Os eixos x e y dividem a circunferência em 4 partes congruentes, chamadas de quadrantes.

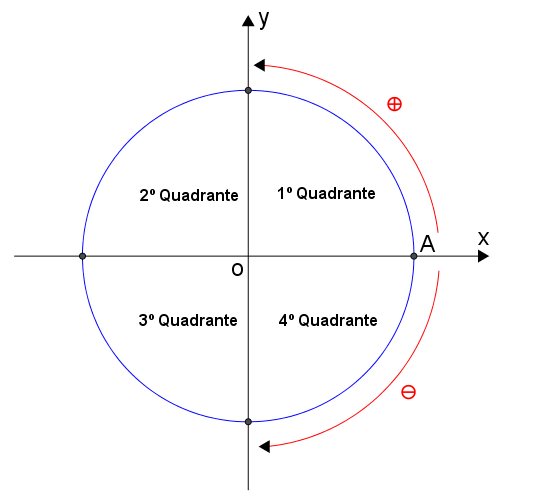
No círculo trigonométrico registramos as medidas dos ângulos que podem estar em graus ou em radianos.

Medida em Graus

A unidade principal de medida de um ângulo é o grau (°).

1° (um grau) equivale a 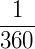$\frac{1}{360}$ de uma circunferência, ou seja, 1° corresponde a uma das 360 partes em que uma circunferência foi dividida. Assim, uma circunferência inteira possui 360°.

Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida minuto ( ‘ ). Um minuto corresponde a 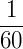$\frac{1}{60}$ de um grau, ou seja, 1 minuto (1’) corresponde a uma das 60 partes em que um ângulo de 1° foi dividido 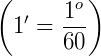$\left( 1^{\prime} = \frac{1^o}{60} \right)$. Assim, um grau possui 60 minutos ($1^o = 60^{\prime}$).

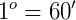Quando queremos expressar medidas de ângulos menores que 1°, utilizamos a medida segundo ( “ ). Um segundo corresponde a 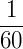$\frac{1}{60}$ de um minuto, ou seja, 1 segundo (1”) corresponde a uma das 60 partes em que um ângulo de 1’ foi dividido 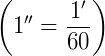$\left( 1^{\prime\prime} = \frac{1^{\prime}}{60} \right)$. Assim, um minuto possui 60 segundos ($1^{\prime} = 60^{\prime\prime}$).

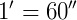Medida em radianos

Arco de 1 radiano (1 rad) é o arco cujo comprimento é igual à medida do raio da circunferência que o contém.

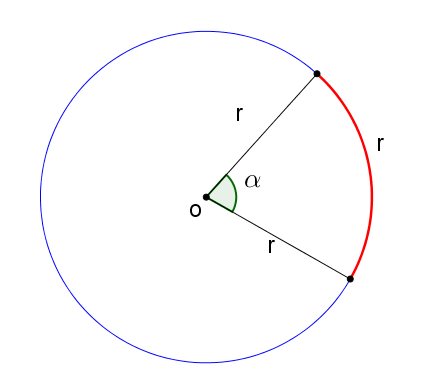
As medidas de arcos de circunferências em graus e em radianos são diretamente proporcionais:

$\frac{360^o}{2\pi} = \frac{180^o}{\pi}$

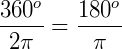
Assim, é possível fazer conversões de unidades através de uma regra de três simples:

$\frac{a}{180^o} = \frac{\alpha}{\pi}$

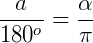
Principais divisões do círculo trigonométrico

Algumas medidas de ângulos são notórias no círculo trigonométrico. São as marcações dos ângulos de 0°, 90°, 180°, 270° e 360°:

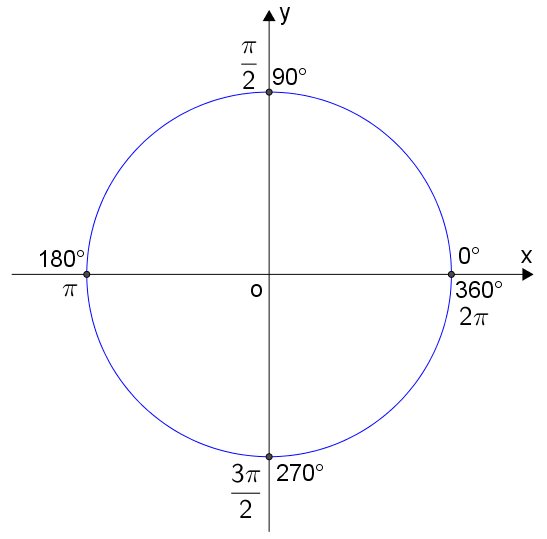
Observe que os valores de 0°, 360° (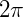$2\pi$) são congruentes.

Arcos côngruos

Toda vez que o ponto da circunferência é o mesmo para dois arcos diferentes (por exemplo, 0 e 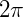$2\pi$), chamamos esses arcos de côngruos ou congruentes. Note que todos os arcos côngruos diferem entre si de um múltiplo de 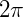$2\pi$, que é o comprimento de cada volta.

Imaginando o ponto como um móvel que se desloca sobre a circunferência no sentido anti-horário, teríamos o seguinte:

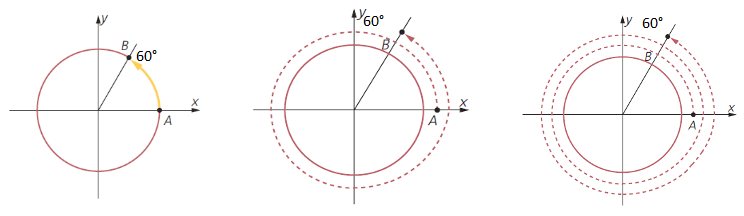
Na primeira figura, o ponto deslocou-se 60° de A até B;

Na segunda figura, o ponto deslocou-se uma volta inteira (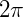$2\pi$ ou 360°) e mais 60°; ou seja, deslocou-se 420°;

Na terceira figura, o ponto deslocou-se duas voltas inteiras (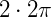$2 \cdot 2\pi$ ou 2 . 360°) e mais 60°; ou seja, 780°.

Supondo que o ponto se deslocasse k voltas inteiras, o número associado à extremidade B do arco AB seria:

$60^o + k \cdot 360^o, k \in \mathbb{Z}$

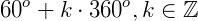
Ou em radianos:

$\frac{\pi}{3} + k \cdot 2 \pi, k \in \mathbb{Z}$

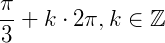
Assim, podemos dizer que dois arcos são côngruos quando suas medidas diferem de um múltiplo de 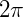$2\pi$ rad ou 360°.

Referências:

DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.

IEZZI, Gelson. Fundamentos de Matemática Elementar. Trigonometria. Vol. 3. São Paulo: Atual, 1995.

REIS, Frederico. Matemática: Arcos e ciclo trigonométrico. Vol. 1. São Paulo: Bernoulli.

Texto originalmente publicado em https://www.infoescola.com/matematica/circulo-trigonometrico/