Conceitualmente, uma equação é chamada de exponencial se as variáveis se encontram no expoente de uma expressão. Para melhor compreensão deste conteúdo, é necessário recordar os conceitos de potenciação e de radiciação. Sendo assim, vamos dar alguns exemplos do que podem ser equações exponenciais:
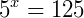
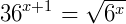
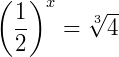
A ideia para resolver equações exponenciais se resume em transforma-las em uma igualdade de potencias de mesma base, ou seja, assumir a forma:
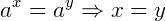
Vamos exemplificar:
1) Vamos resolver a equação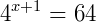 
.
Como devemos igualar as bases de ambos os lados da identidade, podemos dizer que:
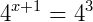
Agora:
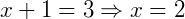
2) Agora, resolveremos .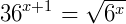
Utilizando algumas propriedades básicas de potências, podemos igualar as bases dessa forma:
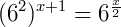
Continuando, temos:
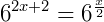
O que nos dá:
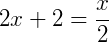
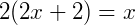
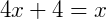
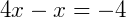
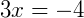
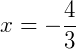
3) Agora,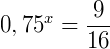 
.
Note na transformação do número decimal para uma fração:
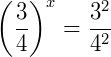
Logo:
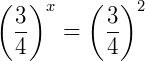
Portando,
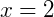
4) Agora, um exemplo um pouco menos intuitivo que também pode ser uma introdução aos logaritmos. Vamos resolver:
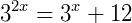
Note que podemos escrever a equação, pela propriedade de potencias, desta maneira:
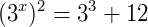
Se fizermos a seguinte substituição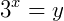 
, podemos reescrever a equação na forma de uma equação do segundo grau:
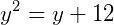
Resolvendo esta equação, temos que existem duas raízes possíveis:
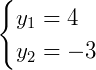
Mas, atenção! Quando substituímos as raízes possíveis na identidade 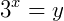nós precisamos verificar se ambas as raízes são válidas, ou seja:
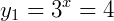
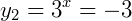
No caso da primeira raiz, é possível que exista 𝑥 que satisfaça a igualdade, que no caso será:
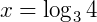
Mas, a segunda raiz não é possível pois, não existe um número que quando elevado a qualquer outro nos retorne um valor negativo:
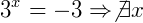
Leia também:
Referências Bibliográficas:
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-exponencial/