Para estudarmos as equações modulares, vamos relembrar o a definição de módulo. Seja um número real 𝑥:
O módulo de um número real 𝑥 é, que é representado por |𝑥| onde:
|𝑥| = 𝑥 se 𝑥 ≥ 0
|𝑥| = −𝑥 se 𝑥 < 0
Podemos também dizer que o módulo de um número real é a “distancia” desse número até o zero da reta real. Por exemplo, a distância do número 4 até o zero seria o seu próprio valor:
|4| = 4
Já a distância do -13 até o zero seria de apenas 13.
|−13| = 13
Propriedades
Algumas propriedades são importantes para aplicamos em soluções de equações modulares. Essas são:
|𝑥| ≥ 0 ∀𝑥 ∈ ℝ
|𝑥| = 0 ⇒ 𝑥 = 0
|𝑥| ≥ 𝑥 ∀𝑥 ∈ ℝ
|𝑥| ≥ |−𝑥| ∀𝑥 ∈ ℝ
|𝑥2| = |𝑥|2 = 𝑥2
|𝑥 + 𝑦| ≤ |𝑥| + |𝑦|
|𝑥 − 𝑦| ≥ |𝑥| − |𝑦|
|𝑥. 𝑦| = |𝑥|. |𝑦|
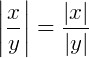
||𝑥| − |𝑦|| ≤ |𝑥 − 𝑦|
Exemplo 1) Vamos resolver a seguinte equação |3𝑥 + 1| = 2:
Pela definição de módulo, podemos dizer que:
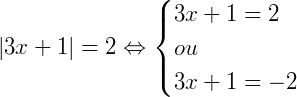
O que nos dá como solução, o valor de 𝑥 nas duas hipóteses, que são equações do primeiro grau:
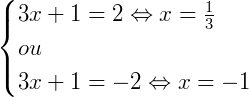
Logo a solução pode ser escrita como:
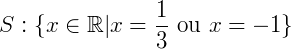
Ou simplesmente:
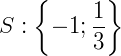
Exemplo 2) Resolveremos agora uma equação modular do 2º grau:
|𝑥2 − 8𝑥 + 13| = 1
Pela definição:
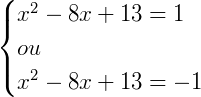
Resolvendo separadamente temos:
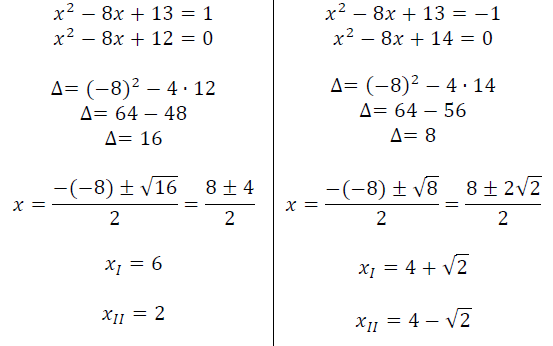
Perceba que neste caso, como tínhamos duas equações do segundo grau como as hipóteses dos dois valores dos módulos, obtemos assim 4 soluções distintas, logo, podemos dizer que a solução geral é a junção de todos os valores de 𝑥:
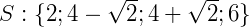
Exemplo 3) Há também equações modulares que possuem mais de uma expressão que estão dentro de um módulo, por exemplo:
|3𝑥 + 2| = |6 − 𝑥|
Neste caso, a definição dos módulos continua valendo, mas é necessário escolher um dos extremos da equação para tomar como o módulo principal, ou seja:
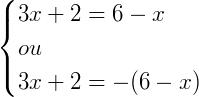
ou também podemos escolher:
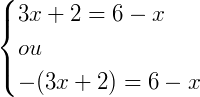
Resolvendo qualquer uma das duas possíveis representações do valor do módulo, o resultado final será o mesmo, basta resolver as equações do primeiro grau para obter os valores:
𝑆: {−4 ; 1}
Referências Bibliográficas
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-modular/