Quando estudamos equações de qualquer natureza podemos encontrar algumas em que não exista uma solução. Exemplos bons são as equações impossíveis e as identidades.
Equações impossíveis
Quando classificamos uma equação como impossível significa que ela não tem uma solução, seja algebricamente ou até por condições previamente estipuladas no problema. Vamos aos exemplos:
1) Se quiséssemos resolver a equação abaixo considerando que 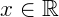 :
:
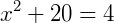
Seria uma equação do 2º aparentemente normal, então, resolvendo:
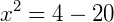
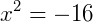
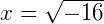
Ora, pela definição de raízes quadradas no domínio dos reais, este valor para 𝑥 não é uma solução. Neste caso dizemos que essa equação é impossível no conjunto dos Reais.
2) Vamos resolver a equação abaixo:
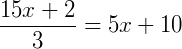
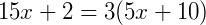

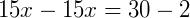
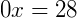
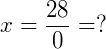
Vemos que não é possível encontrarmos um valor para 𝑥 nesta igualdade. O que torna esta equação impossível.
Equações identidades
As equações identidades são aquelas em que se admitem infinitas soluções. Damos o nome de identidades pois geralmente ambos os lados da igualdade são idênticos em algum momento ao desenvolver a equação. Vejamos:
1) Supondo que quiséssemos desenvolver esta equação abaixo a fim de encontrar um valor para x:
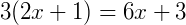
Faríamos normalmente a distributiva e encontraríamos:
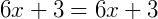
Note que ambos os lados da equação já são idênticos. Neste caso já temos uma equação identidade que assume infinitas soluções.
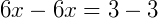
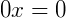
Referências Bibliográficas:
GONÇALVES, Adilson. Introdução à Álgebra. Rio de Janeiro: IMPA, 1999.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacoes-impossiveis-e-identidades/