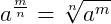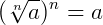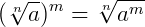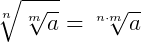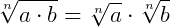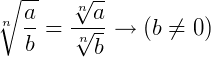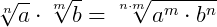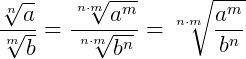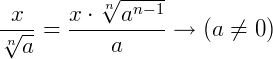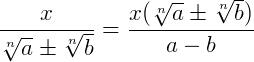Quando dizemos que uma equação é irracional significa que ao menos uma de suas variáveis estão no radicando. Em outras palavras, as variáveis estão dentro de uma raiz de qualquer índice.
Vamos relembrar algumas propriedades de radiciação com números, ainda sem incógnitas, onde os números 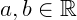 e os índices
e os índices 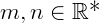 . Não é necessário decorar estas propriedades, porém elas podem ser de grande ajuda ao solucionar equações irracionais:
. Não é necessário decorar estas propriedades, porém elas podem ser de grande ajuda ao solucionar equações irracionais:
Propriedades da radiciação
Agora, vamos dar um exemplo de cada uma destas propriedades quando as incógnitas aparecem no radicando.
Exemplo 1: Vamos encontrar a solução desta equação: 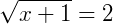
Utilizando a propriedade (2), podemos então elevar ambos os lados da equação pelo mesmo índice da raiz, onde temos:
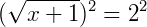
Pela propriedade (2) a raiz quadrada será eliminada. Então, resolvendo:
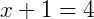
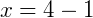
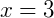
Exemplo 2: Equações irracionais podem aparecer na forma de uma equação exponencial, ou seja, a variável encontra-se no índice de uma raiz. Seja a equação 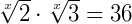 . Vamos solucioná-la:
. Vamos solucioná-la:
Utilizando a propriedade (5), podemos reescrevê-la como:
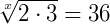
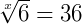
Elevando a x os dois membros da igualdade, temos:
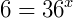
Como 36 = 6² podemos dizer que:
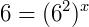
Pela propriedade das potências de potências, podemos multiplicar o 2 pelo x que estão elevando o 6, o que nos garante escrever:
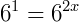
Ora, pela igualdade, dizemos que:
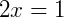
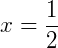
Exemplo 3: Agora temos 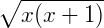 . Para solucioná-la, ainda utilizando a propriedade (2), podemos eliminar a raiz elevando ao quadrado ambos os lados da equação, o que nos traz:
. Para solucioná-la, ainda utilizando a propriedade (2), podemos eliminar a raiz elevando ao quadrado ambos os lados da equação, o que nos traz:
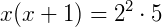
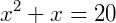
Obtemos uma equação do segundo grau, e resolvendo temos:
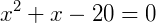
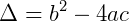
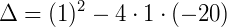
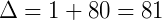
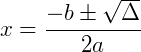
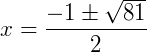
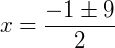
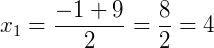
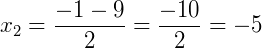
Com isso, sabemos que o valor de x na equação pode ser 4 ou – 5.
Exemplo 4: Agora vamos obter a solução de 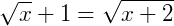 . Podemos elevar ao quadrado os dois membros da igualdade, o que nos resulta em:
. Podemos elevar ao quadrado os dois membros da igualdade, o que nos resulta em:
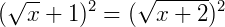
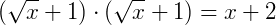
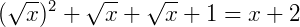
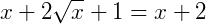
Isolando as variáveis temos:
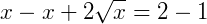
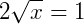
Então:
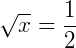
Elevando mais uma vez os membros ao quadrado chegamos a:
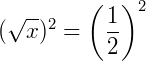
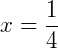
Condição de existência de radicais
Se utilizarmos sempre as propriedades da radiciação, encontrar uma solução de uma equação irracional não se torna uma tarefa difícil. Vale lembrar que o conjunto de solução de uma equação deve ser sempre levado em conta. Como quase sempre a solução de uma equação irracional está contida nos reais então é necessário atentar-se a sua condição de existência. Raízes com índices pares de números negativos não existem nos reais:
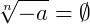 para n = 2, 4, 6 ...
para n = 2, 4, 6 ...
Já com índices impares é possível. No caso:
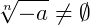 para n = 3, 5, 7...
para n = 3, 5, 7...
Referências Bibliográficas
GONÇALVES, Adilson. Introdução à Álgebra. Rio de Janeiro: IMPA, 1999.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacoes-irracionais/