Equações trigonométricas - como calcular, exemplos

Ouça este artigo:

Uma equação trigonométrica é aquela onde a incógnita aparece na forma da medida de arcos ou nos ângulos de uma função trigonométrica. São exemplos de equações trigonométricas: 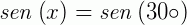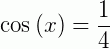$\mathit{sen}\left(x\right)=\mathit{sen}\left(30\circ \right)$ , $\cos \left(x\right)=\frac{1}{4}$ e $\mathit{tg}\left(x\right)=\sqrt{3}$ .

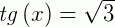Vejamos as principais formas das equações trigonométricas e algumas formas de resolvê-las, através de exemplos.

Conteúdo deste artigo

Equações da forma sen(x) = a, cos(x) = a e tg(x) = a
Equações da forma sen(x) = sen(a), cos(x) = cos(a) e tg(x) = tg(a)
Exercícios

Equações da forma sen(x) = a, cos(x) = a e tg(x) = a

Para resolver esse tipo de equação precisamos lembrar que temos duas opções possíveis: quando o problema nos fornece o intervalo e quando ele não oferece. No primeiro caso, apenas verificamos no intervalo fornecido no circulo trigonométrico quantos ângulos têm aquele seno, cosseno ou tangente. No segundo caso, precisamos apresentar a resposta de maneira geral, para n voltas no circulo trigonométrico.

Exemplo

1) Resolva a equação 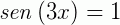$\mathit{sen}\left(3x\right)=1$ , para n voltas e para o intervalo $0\le x\le \pi$ .

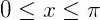Solução:

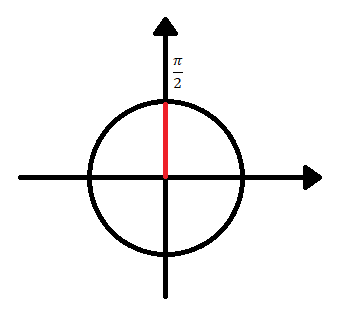
Começamos encontrando um ângulo conhecido que sabemos ter seno = 1, ou seja, 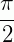$\frac{\pi }{2}$ . Em seguida, igualamos a variável a esse ângulo:* Para o intervalo 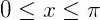$0\le x\le \pi$ (ou para 1 volta no ciclo trigonométrico, nesse caso é o mesmo) no ciclo trigonométrico: 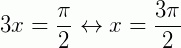$3x=\frac{\pi }{2}\leftrightarrow x=\frac{3\pi }{2}$ .* Para n voltas no ciclo trigonométrico: 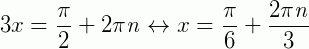$3x=\frac{\pi }{2}+2\mathit{\pi n}\leftrightarrow x=\frac{\pi }{6}+\frac{2\mathit{\pi n}}{3}$ para $n\epsilon Z$ .

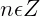Logo temos: 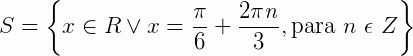$S=\left\lbrace x\in R\vee x=\frac{\pi }{6}+\frac{2\mathit{\pi n}}{3},\text{para }n\text{ }\epsilon\text{ }Z\right\rbrace$ .

Observação: Se tivéssemos dois ângulos onde isso é verdade, então a solução seria dada em função dos dois.

Equações da forma sen(x) = sen(a), cos(x) = cos(a) e tg(x) = tg(a)

Aqui a ideia é quase a mesma, porém agora vamos igualar diretamente a variável ao arco desejado.

Exemplo

1) Resolva a equação 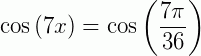$\cos \left(7x\right)=\cos \left(\frac{7\pi }{36}\right)$ .

Solução:

Vamos iniciar descobrindo em qual quadrante o ângulo 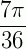$\frac{7\pi }{36}$ está. Para isso basta converter isso de radianos para graus, onde encontraremos 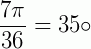$\frac{7\pi }{36}=35\circ$ , ou seja, ele está no 1° quadrante.

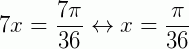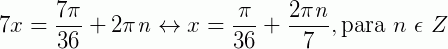Vamos lembrar que no 1° quadrante seno e cosseno são positivos, então não precisamos mudar nenhum sinal. Com isso temos que:* Para 1 volta no ciclo trigonométrico: $7x=\frac{7\pi }{36}\leftrightarrow x=\frac{\pi }{36}$ * Para n voltas no ciclo trigonométrico: $7x=\frac{7\pi }{36}+2\mathit{\pi n}\leftrightarrow x=\frac{\pi }{36}+\frac{2\mathit{\pi n}}{7},\text{para }n\text{ }\epsilon\text{ }Z$ .

Logo temos: 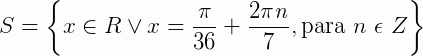$S=\left\lbrace x\in R\vee x=\frac{\pi }{36}+\frac{2\mathit{\pi n}}{7},\text{para }n\text{ }\epsilon\text{ }Z\right\rbrace$ .

Podemos também ter expressões misturando os dois casos vistos acima.

Exercícios

1) (FATEC - adaptado) O conjunto solução da equação 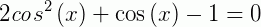$2\mathit{co}{s}^{2}\left(x\right)+\cos \left(x\right)-1=0$ , no universo 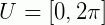$U=\left\lbrack \mathrm{0,2}\pi \right\rbrack$ é?

Solução:

Fazendo a mudança de variável $u=\cos \left(x\right),$ temos que:

$2\mathit{co}{s}^{2}\left(x\right)+\cos \left(x\right)-1=0\leftrightarrow 2{u}^{2}+u-1=0\leftrightarrow u=\frac{-1\pm 3}{4}$

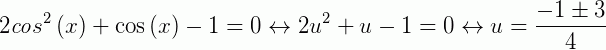
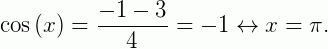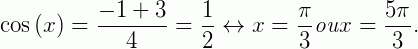
Logo, retornando a variável x, e levando em conta nosso universo (intervalo):* $\cos \left(x\right)=\frac{-1-3}{4}=-1\leftrightarrow x=\pi \mathrm{.}$ * $\cos \left(x\right)=\frac{-1+3}{4}=\frac{1}{2}\leftrightarrow x=\frac{\pi }{3}\mathit{ou}x=\frac{5\pi }{3}\mathrm{.}$

Assim, o conjunto solução será 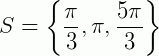$S=\left\lbrace \frac{\pi }{3},\pi ,\frac{5\pi }{3}\right\rbrace$ .

2) (UFRGS - adaptado) O número de soluções da equação 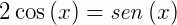$2\cos \left(x\right)=\mathit{sen}\left(x\right)$ , no intervalo 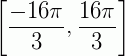$\left\lbrack \frac{-16\pi }{3},\frac{16\pi }{3}\right\rbrack$ é?

Solução:

Dividindo os dois lados da equação por cos(x) e manipulando algebricamente: $2\cos \left(x\right)=\mathit{sen}\left(x\right)\leftrightarrow \frac{2\cos \left(x\right)}{\cos \left(x\right)}=\frac{\mathit{sen}\left(x\right)}{\cos \left(x\right)}\leftrightarrow \mathit{tg}\left(x\right)=2$ .

Como tg(x) é positivo, temos x está no 1° ou 3° quadrantes, ou seja, temos duas soluções por volta. Mas, de 0 até 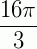$\frac{16\pi }{3}$ temos 2,5 voltas, ou seja, no intervalo 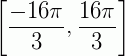$\left\lbrack \frac{-16\pi }{3},\frac{16\pi }{3}\right\rbrack$ teremos 5 voltas. Como temos 2 soluções por voltas, teremos no total 10 soluções.