Fatorial

O conceito de fatorial é muito utilizado no estudo de arranjos e permutações, a fim de facilitar os cálculos. A ideia é bastante simples e de fácil compreensão.

O fatorial de um número inteiro m não negativo, é indicado por m! (lê-se “m fatorial”) e é definido pela relação:

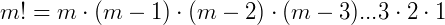$m! = m \cdot (m-1) \cdot (m-2) \cdot (m-3) ... 3 \cdot 2 \cdot 1$, para m ≥ 2.

Algumas definições são:

• 1! = 1
• 0! = 1

Exemplos:

• 3! = 3 . 2 . 1 = 6
• 4! = 4 . 3 . 2 . 1 = 24
• 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720

Veja que o cálculo do fatorial se torna trabalhoso a medida que m aumenta, veja:

• 10! = 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3.628.800

Assim, podemos simplificar alguns cálculos, usando o artifício de não calcular totalmente o fatorial, mas sim uma parte dele:

(n+1)! = (n+1) . n . (n-1) . (n-2) ... 3 . 2 . 1 = (n+1) . n!

Por exemplo:

10! = 10 . 9 . 8 . 7!

Exemplos

1. Calcule 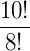$\frac{10!}{8!}$

Fazemos: 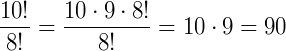$\frac{10!}{8!} = \frac{10 \cdot 9 \cdot 8!}{8!} = 10 \cdot 9 = 90$

2. Calcule 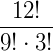$\frac{12!}{9! \cdot 3!}$

Fazemos: 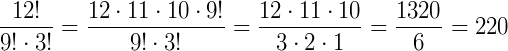$\frac{12!}{9! \cdot 3!} = \frac{12 \cdot 11 \cdot 10 \cdot 9!}{9! \cdot 3!} = \frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1} = \frac{1320}{6} = 220$

Cuidado

As seguintes operações não são válidas:

• n! + x! = (n+x)!
• n! - x! = (n-x)!
• n! . x! = (n . x)!

Referências:

RIBEIRO, Paulo Vinícius; PAULO, Luiz. Matemática: Princípio fundamental da contagem e arranjos. Vol. 4. São Paulo: Bernoulli.

HAZZAN, Samuel. Fundamentos de Matemática Elementar. Combinatória. Probabilidade. Vol. 5. São Paulo: Atual, 1997.

Texto originalmente publicado em https://www.infoescola.com/matematica/fatorial/