Função identidade

Uma função identidade (ou função inclusão) é uma função que possui a imagem de cada elemento como o próprio elemento. Uma função identidade é necessariamente bijetora, o que remete a sua definição. Relembrando, uma função é dita bijetora quando a mesma é injetora e sobrejetora. Vamos formalizar o conceito apresentado:

Dado um conjunto 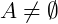$A \neq \emptyset$, a aplicação 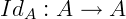$Id_A : A \rightarrow A$ dada pela lei 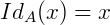$Id_A (x) = x$ é chamada função identidade do conjunto A. Para cada conjunto A existe uma função identidade e, assim, se 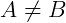$A \neq B$, então $Id_A \neq Id_B$.

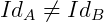Proposição: Se é uma função bijetora, então as composições f o f^-1 = Id_A e também f^-1 o f = Id_B. Vamos demonstrar:

1. Se f é uma aplicação bijetora, então, pela definição de função inversa, 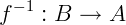$f^{-1} : B \rightarrow A$.

2. Dado um 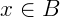$x \in B$, temos:

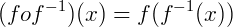$(f o f^{-1})(x) = f(f^{-1}(x))$ portanto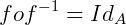 $f o f^{-1} = Id_A$

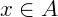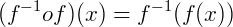 3. Agora, dado um $x \in A$:

$(f^{-1} o f)(x) = f^{-1}(f(x))$ portanto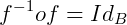 $f^{-1} o f = Id_B$

Nota: Em Álgebra, dizemos que as funções identidade são elementos neutros na operação de composição de funções.

Gráfico das Funções Identidade

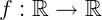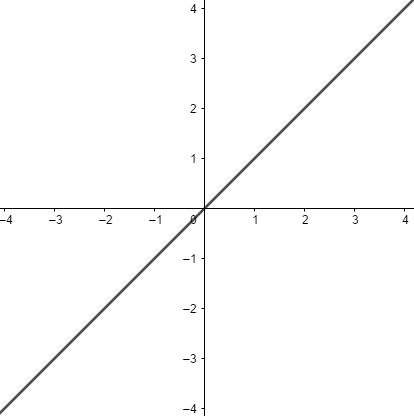
Seja uma função $f : \mathbb{R} \rightarrow \mathbb{R}$ definida por 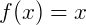$f(x) = x$. Então pela definição de funções afim, a=1 e b=0, o gráfico de uma função identidade é chamada de bissetriz dos quadrantes impares, que passam pelo 1º e 3º quadrante e na origem do eixo cartesiano (0, 0).

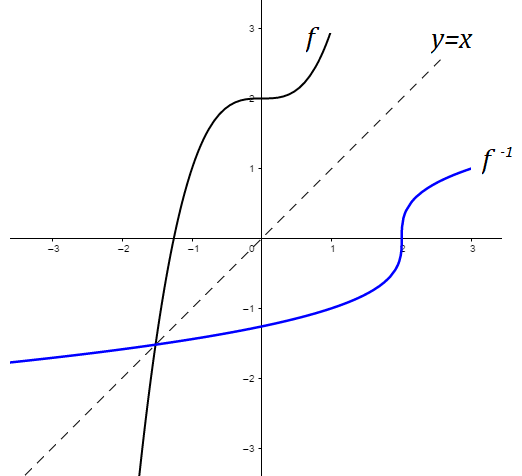
No estudo das funções inversas, podemos observar que a função identidade divide o gráfico de f e f^-1 de uma forma simétrica em relação a reta y=x. Observe o exemplo abaixo:

Referências Bibliográficas:

LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.

DOMINGUES, Hygino H; IEZZI, Gelson. Álgebra Moderna. São Paulo: Editora Atual, 1982.

Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-identidade/