Função polinomial

Uma função é dita polinomial quando dado uma função 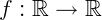$f : \mathbb{R} \rightarrow \mathbb{R}$ a sua lei é dada por um polinômio de grau n. Relembrando o conceito de polinômios, podemos representar uma função polinomial de uma forma genérica como:

$f(x) = a_n x^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1 x^1 + a_0 x^0$

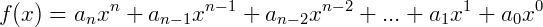
Ou ainda, pela notação de somatório:

$\displaystyle f(x) = \sum_{i=0}^n a_i x^i$

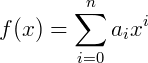
Onde a_n, a_n-1, a_n-2, ... a₁ e a₀ e são as constantes que chamamos de coeficientes do polinômio e xⁿ, x^n-1, ... x⁰ são as variáveis da função.

Grau

O grau de uma função polinomial é classificado pelo valor do expoente n a variável x do polinômio, sendo que deve ser um inteiro positivo e maior ou igual a zero, ou seja: 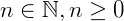$n \in \mathbb{N}, n \geq 0$.

Exemplo 1) Funções afim são funções polinomiais do primeiro grau. Note que o expoente de x na função é igual a 1:

$f(x) = a_1 x^1 + a_0 x^0$

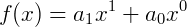
Ou pode ser escrita como:

$f(x) = ax+b$

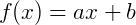
Note que o termo constante b é igual a 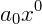$a_0 x^0$.

Exemplo 2) Funções quadráticas são classificadas como funções de grau 2, ou funções do 2º grau. Veja:

$f(x) = a_2 x^2 + a_1 x^1 + a_0 x^0$

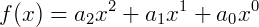
Ou também:

$f(x) = ax^2 + bx + c$

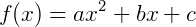
Neste caso 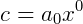$c = a_0 x^0$.

Exemplo 3) Uma função do terceiro grau, naturalmente é escrita como:

$f(x) = a_3 x^3 + a_2 x^2 + a_1 x^1 + a_0 x^0$

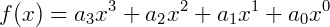
Outra forma:

$f(x) = ax^3 + bx^2 + cx + d$

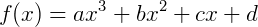
Exemplo 4) Funções constantes, aquelas em que não possuem variáveis, são classificadas como funções de grau zero. Note:

$f(x) = a_0 x^0 = a_0$

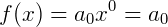
Exemplo 5) Uma função do tipo 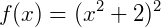$f(x) = (x^2 + 2)^2$ é de quarto grau, pois, desenvolvendo o produto temos:

$f(x) = x^4 + 4x^2 + 4$

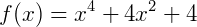
Referências Bibliográficas:

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-polinomial/