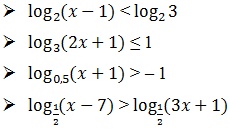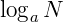Inequação logarítmica

O cálculo logarítmico surgiu no século XVII com a grande expansão do comércio, assim como da evolução científica. Durante os três primeiros séculos a partir dali, o cálculo logarítmico – e exponencial – tornou-se uma ferramenta de suporte par cálculos mais sofisticados. A ideia dos logarítmicos era tornar simples operações complexas de multiplicação e divisão. Muito da evolução da matemática e das ciências que dela dependem é atribuído aos logaritmos.

Inequação logarítmica

Uma desigualdade cuja incógnita aparece no logaritmando ou na base de ao menos um dos logaritmos é chamada de inequação logarítmica. Veja os exemplos:

Resolução de inequações logarítmicas

A resolução de uma inequação logarítmica depende de alguns fatores. Siga os passos seguintes:

• Condição de existência: antes de prosseguir com a resolução, procure a (s) condição (ões) de existência (s) dos logaritmos. Lembre-se de que em  , a > 0 e a ≠ 1, N > 0. Essas são as condições de existência.
• Base: caso alguma base seja diferente, converta-a a mesma base e em seguida forme uma inequação com logaritmandos.
• Função crescente: se a > 1, mantem-se a direção do sinal inicial.
• Função decrescente: se 0 < a < 1, inverte a direção do sinal inicial.
• Solução final: a solução é dada pela interseção das condições de existência pelo resultado da inequação.

Para praticar os passos anteriores, vamos resolver as inequações exemplificadas no início deste trabalho.

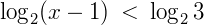
Condição de existência:

x – 1 > 0 →  x > 1  (S₁)

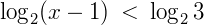  → como a > 1 mantem-se a direção inicial do sinal.

x – 1 < 3

x < 4   (S₂)

S = S₁ ∩ S₂ → a solução final é a interseção das soluções 1 e 2.

S = {x ∈ R | 1 < x < 4}

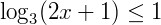
Condição de existência:

2x + 1 > 0 → 2x > – 1 → x = 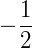    (S₁)

Veja que no 2º membro da desigualdade não temos um logaritmo. Porém, podemos escrever o número 1 em forma de logaritmo, dessa forma igualando as bases: 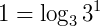. A Base 3 foi escrita intencionalmente, para se igualar a base do logaritmo escrito no 1º membro. Reescrevendo a inequação:

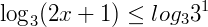 → como a > 1 mantem-se a direção inicial do sinal.

2x + 1 ≤ 3¹ → 2x ≤ 3 – 1

2x ≤ 2 → x ≤ 1.

S = S₁ ∩ S₂  → a solução final é a interseção das soluções 1 e 2.

S = {x ∈ R | 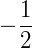  < x ≤ 1}

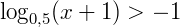
Condição de existência:

x + 1 > 0 → x > – 1   (S₁)

Da mesma forma que na inequação anterior, podemos escrever o – 1 na forma de logaritmo. Mas antes perceba que (0,5) = . Desta forma, escreve-se –1 em forma de logaritmo na base : 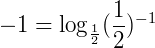. Reescrevendo a inequação:

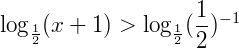 → como 0 < a < 1, inverte-se a direção inicial do sinal.

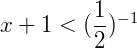 → x + 1 < 2

x < 2 – 1 → x < 1   (S₂)

S = S₁ ∩ S₂  → a solução final é a interseção das soluções 1 e 2.

S = {x ∈ R | – 1 < x < 1}

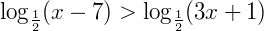
Condições de existência:

x – 7 > 0 → x > 7   (S₁)

3x + 1 > 0 → 3x > – 1 → x > 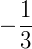 (S₂)

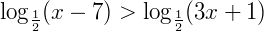 → como 0 < a <1 inverte-se a direção inicial do sinal.

x – 7 < 3x + 1   →   x – 3x < 1 + 7

–2x < 8 → 2x > – 8 →  x > – 4    (S₃)

S = S₁ ∩ S₂ ∩ S₃    →     a solução final é a interseção das soluções 1, 2 e 3.

S = {x ∈ R | x > 7}

“Recomece sempre que precisar, pois a cada recomeço nascem novas esperanças de sucesso”.
(Robison Sá)

Referências bibliográficas:
YOUSSEF, Antonio Nicolau (et al.). Matemática: ensino médio, volume único. – São Paulo: Scipione, 2005.
IEZZI, Gelson (et al.). Matemática: ciência e aplicações, 1: ensino médio. – 6. ed. – São Paulo: Saraiva, 2010.