Uma inequação é uma sentença matemática expressa por uma desigualdade. Assim, em uma inequação trigonométrica temos uma desigualdade onde a incógnita aparece na forma da medida de arcos ou nos ângulos de uma função trigonométrica. São exemplos:
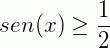
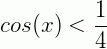
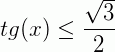
Não existe um padrão de resolução, por isso o melhor jeito de entender como resolvê-las é através de exemplos. Dá mesma forma que a equação trigonométrica se as questões não apresentarem um intervalo de resolução é necessário apresentar uma solução geral para n voltas no círculo trigonométrico. Vejamos alguns exemplos.
Exemplos:
1) Resolva a inequação 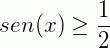 no intervalo
no intervalo 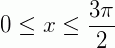 .
.
Solução:
Em primeiro lugar, precisamos encontrar os valores onde isso seria uma igualdade (dentro do nosso intervalo), ou seja:
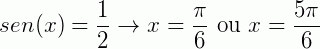
(o primeiro é um ângulo notável e o segundo é o seu correspondente no 2° quadrante).
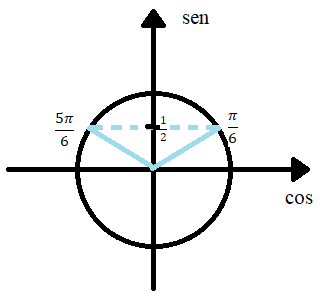
Em seguida, encontramos os possíveis ângulos no círculo trigonométrico (ver figura acima). Analisar os ângulos onde a desigualdade é verdadeira, ou seja, 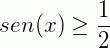 . Isso ocorre, no nosso intervalo, quando o ângulo é maior que
. Isso ocorre, no nosso intervalo, quando o ângulo é maior que 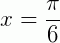 e quando o ângulo é menor que
e quando o ângulo é menor que 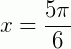 (ver figura abaixo).
(ver figura abaixo).
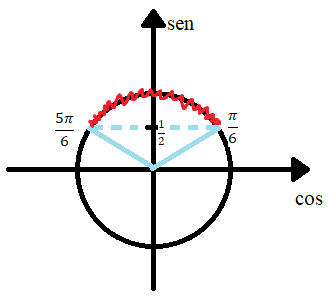
Logo a solução será:
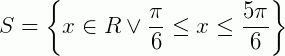
2) Resolva a inequação 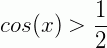 .
.
Solução:
Em uma volta, ou seja, no intervalo 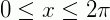 ,
, 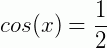 quando
quando 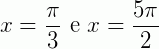 (o primeiro é um ângulo notável e o segundo é o seu correspondente no 4° quadrante). Lembrando que cosseno aumenta conforme o ângulo aumenta no 1° e no 4° quadrantes, temos que
(o primeiro é um ângulo notável e o segundo é o seu correspondente no 4° quadrante). Lembrando que cosseno aumenta conforme o ângulo aumenta no 1° e no 4° quadrantes, temos que 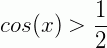 de 0 até
de 0 até 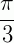 e de
e de 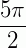 até
até 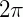 . Abaixo desenhamos isso no circulo trigonométrico.
. Abaixo desenhamos isso no circulo trigonométrico.
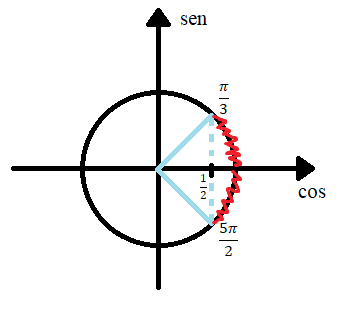
Escrevendo isso para n voltas, temos que a solução será:
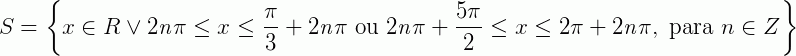
3) Resolva a inequação 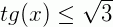 no intervalo
no intervalo 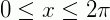 .
.
Lembrando que 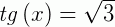 quando
quando 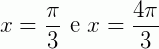 (o primeiro é um ângulo notável e o segundo é o seu correspondente no 3° quadrante). Abaixo temos um esboço disso nos eixos.
(o primeiro é um ângulo notável e o segundo é o seu correspondente no 3° quadrante). Abaixo temos um esboço disso nos eixos.
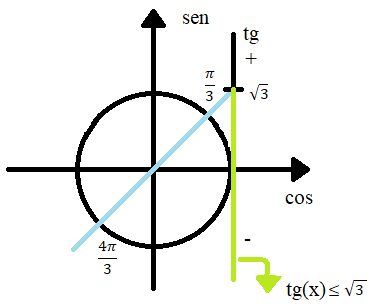
Como temos que 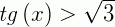 (o que não queremos) nos intervalos
(o que não queremos) nos intervalos 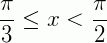 e
e 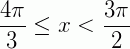 , então nosso resultado estará no restante do intervalo do círculo (como descrito na figura abaixo).
, então nosso resultado estará no restante do intervalo do círculo (como descrito na figura abaixo).
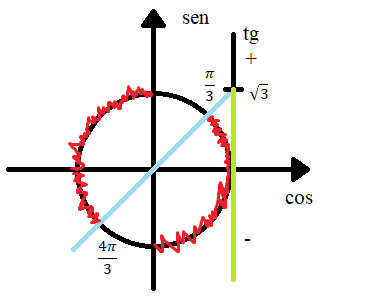
Logo a solução será:
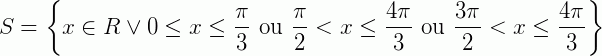
4) (UEG – adaptado) Qual o conjunto solução da inequação  , no intervalo
, no intervalo 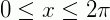 , para x real?
, para x real?
Solução:
Lembrando que
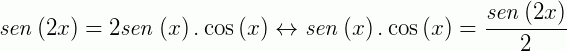
Logo:
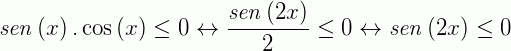
Mas, 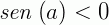 no 3° e 4° quadrantes, ou seja, no intervalo
no 3° e 4° quadrantes, ou seja, no intervalo 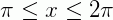 e
e 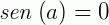 quando
quando 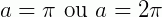 .
.
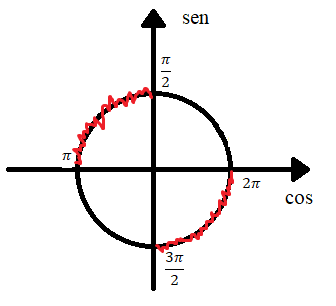
Logo, se a = 2x o conjunto solução será:
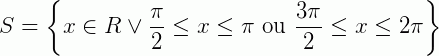
Texto originalmente publicado em https://www.infoescola.com/matematica/inequacoes-trigonometricas/