O logaritmo surgiu em 1614 numa publicação de John Napier, denominada Mirifici Logarithmorum Canonis Descriptio. John Napier era escocês, nascido em 1550. Ficou muito famoso na matemática, principalmente com a invenção do logaritmo. É por conta dele que o logaritmo natural também é conhecido como logaritmo neperiano.
A definição de logaritmo diz que sendo a e b números reais positivos, chama-se logaritmo de b na base a, o expoente em que a deve ser elevado de modo que a potência obtida de base a seja igual a b.

Com 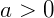 ,
, 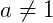 e
e 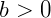 .
.
Assim, o logaritmo nada mais é que um expoente. Dizemos que a é a base do logaritmo, b é o logaritmando e x é o logaritmo.
Conteúdo deste artigo
Definição do logaritmo natural
O logaritmo natural de um número a, a > 0, é o logaritmo desse número a, na base e. Representamos o logaritmo natural por ln. Assim:
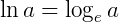
O número e
O número e é chamado de número de Euler por conta de Leonhard Euler. Ele foi um dos matemáticos mais brilhantes da sua época e posterior. Seu nome ficou ligado para sempre ao número irracional e, cujo valor é aproximadamente 2,71.
Assim, o logaritmo natural de um número, é o logaritmo desse número na base igual a 2,71, ou na base e.
Definições
Assim como no estudo dos logaritmos, podemos estabelecer algumas definições sobre o logaritmo natural:
I) 
Usando a definição de logaritmo natural, temos que 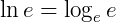
Usando a definição de logaritmo, temos: 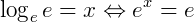
Pelas propriedades da potenciação, se as bases são iguais, os expoentes também são, assim, x = 1 e 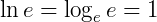
II) 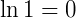
Usando a definição de logaritmo natural, temos que 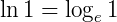
Usando a definição de logaritmo, temos: 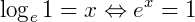
Pelas propriedades da potenciação, todo número elevado a potência 0 é igual a 1, assim, x = 0 e 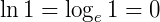
III) 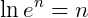
Usando a definição de logaritmo natural, temos que 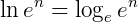
Uma das propriedades do logaritmo diz que o logaritmo de uma potência é igual ao produto entre o expoente da potência e o logaritmo cujo logaritmando é a base da potência. Assim, 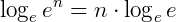 .
.
Como 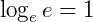 , temos que
, temos que 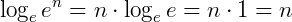 .
.
Propriedades
As propriedades principais do logaritmo também estão garantidas para o logaritmo natural.
I) Logaritmo natural do produto
O logaritmo natural de um produto é igual à soma dos logaritmos naturais:

II) Logaritmo natural do quociente
O logaritmo natural de um quociente é igual à diferença dos logaritmos naturais:
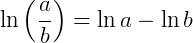
III) Logaritmo natural de uma potência
O logaritmo natural de uma potência é igual ao produto do expoente pelo logaritmo natural da base dessa potência.
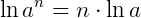
Mudança de base
Em um logaritmo natural, a base é e. Podemos mudar da base para a base decimal (10). Veja:
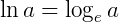
Mudando para a base 10:
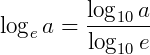
Como 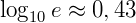 , temos:
, temos:
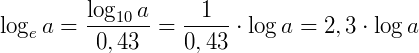
Portanto, podemos realizar uma mudança de base considerando sempre a relação
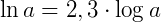
Exemplos
1. Sabendo que log 7 = 0,84, determine ln 7.
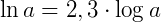
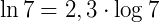
Como log 7 = 0,84, então:
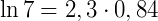
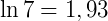
2. Dados log e = 0,43 e log 4 = 0,60, calcule o valor de x na equação 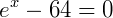 .
.
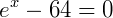
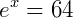
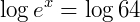
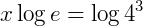
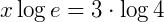
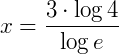
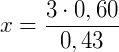
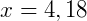
Referência:
BOYER, Carl B. História da Matemática. Trad. Elza F. Gomide. SP: Editora Edgard Blücher Ltda, 2012.
Texto originalmente publicado em https://www.infoescola.com/matematica/logaritmo-natural/