Matriz Adjunta

Por Mauricio P Marques Fernandes

A matriz adjunta é o nome que se dá a matriz quadrada que se obtém fazendo transposta das matrizes dos cofatores de uma matriz original. Indicamos a matriz adjunta com um traço sobre a letra que indica a Matriz.

Exemplos:

1. A é a matriz adjunta A
2. B é a matriz adjunta B

Para determinar a matriz adjunta A é necessário primeiro obtermos a matriz dos cofatores, representada geralmente por C, de uma matriz original, isto é, para se obter a matriz adjunta de A, precisamos antes encontrar a matriz dos cofatores de A para então determinarmos a matriz adjunta A.

Por exemplo, se a matriz dos cofatores de A for a matriz 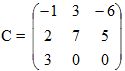 , então a matriz adjunta de A será:

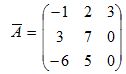
Utilidade da Matriz Adjunta

A Matriz adjunta é útil na determinação da matriz inversa quando calculada pela fórmula .

Exemplo:

Calcular a matriz inversa de A, sabendo que a matriz dos cofatores de A é 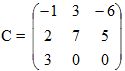 e que o determinante de A é det (A) = 3 .

Sendo a matriz adjunta A a transposta da matriz C dos cofatores, então A = C^t.

Assim, temos:

A = C^t

Substituindo a matriz C e calculando sua transposta obtemos:

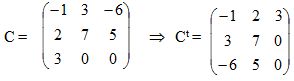
Assim, concluímos que a matriz adjunta de A é .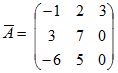

Como já temos o determinante de A e a matriz adjunta de A podemos enfim calcular a matriz inversa de A^-1 substituindo os valores na fórmula .

Assim, temos:

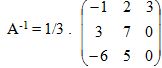
Multiplicando os elementos de A por 1/3, obtemos a matriz inversa de A.

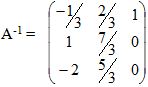
Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-adjunta/