Uma matriz é chamada de inversível ou não singular se, e somente se, seu determinante é diferente de zero, por isso uma matriz só pode ser inversível se for uma matriz quadrada com determinante diferente de zero e é representada pelo número -1 sobrescrito ao nome da matriz. Exemplos:
- A-1 é a representação da matriz inversa de A
- B-1 é representação da matriz inversa de B
Um método para determinar a matriz inversa é chamado de método de inversão por matriz adjunta. É um método mais longo que o método por sistemas lineares, porém, mais simples, pois não recaem em n sistemas de n equações. A utilização desse método depende do teorema 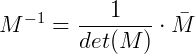 , onde:
, onde:
- M-1 é a matriz inversa de M.
- det(M) é o determinante da matriz M
- M é a matriz adjunta de M.
O método por matriz adjunta é constituído pela seguinte sequência de ações:
- Calcular o determinante da Matriz M.
- Calcular a matriz C dos cofatores de M.
- Determinar a matriz adjunta M
- Calcular

Antes de tomarmos um exemplo qualquer, devemos observar que só existirá a matriz inversa de M se o seu determinante for diferente de zero, caso contrário teremos uma divisão por zero no passo 4 da sequência anterior, o que não é permitido. Vamos calcular, como exemplo, a inversa, se houver, da matriz 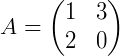 . Seguindo a sequência dada, temos:
. Seguindo a sequência dada, temos:
1. Cálculo do determinante de A:
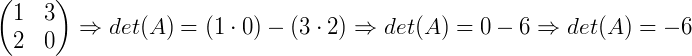
O determinante de A é diferente de zero, isso significa que existe a matriz inversa A-1. Passamos então para o passo seguinte. 2. Cálculo da matriz C dos cofatores de A. Seja A, a matriz 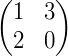 , então a matriz C dos cofatores de A é
, então a matriz C dos cofatores de A é 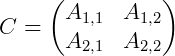 .
.
Cofator Ai,j do elemento a11 (1):
![]() Cofator Ai,j do elemento a12 (3):
Cofator Ai,j do elemento a12 (3): ![]() Cofator Ai,j do elemento a21 (2):
Cofator Ai,j do elemento a21 (2): ![]() Cofator Ai,j do elemento a22 (0):
Cofator Ai,j do elemento a22 (0): ![]() De posse dos valores dos cofatores escrevemos a matriz C dos cofatores:
De posse dos valores dos cofatores escrevemos a matriz C dos cofatores: 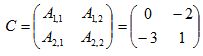 3. Cálculo da matriz Adjunta de A.A matriz adjunta A é a transposta da matriz C dos cofatores, isto é: A = Ct Portanto temos:
3. Cálculo da matriz Adjunta de A.A matriz adjunta A é a transposta da matriz C dos cofatores, isto é: A = Ct Portanto temos: 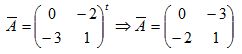 4. Cálculo da inversa A-1, pelo teorema
4. Cálculo da inversa A-1, pelo teorema ![]() Substituindo os valores encontrados anteriormente no teorema temos:
Substituindo os valores encontrados anteriormente no teorema temos: 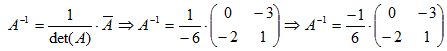 Multiplicando
Multiplicando 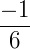 pelos elementos da matriz A, obtemos enfim a inversa de A.
pelos elementos da matriz A, obtemos enfim a inversa de A. 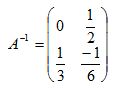
Texto originalmente publicado em https://www.infoescola.com/matematica/matriz-inversa-inversao-por-matriz-adjunta/