Máximo Divisor Comum (MDC) - Matemática

Sejam os números 12, 18 e 30 e os conjuntos D(12), D(18) e D(30) de seus respectivos divisores, que são finitos e ordenados.

D(12) = {1, 2, 3, 4, 6, 12}
D(18) = {1, 2, 3, 6, 9, 18}
D(30) = {1, 2, 3, 5, 6, 10, 15, 30}

Considerando agora o conjunto dos divisores comuns, isto é, o conjunto interseção de D(12), D(18) e D(30).

D(12) ∩ D(18) ∩ D(30) = {1, 2, 3, 6}

que é um conjunto finito e ordenado.

Como:

Todo conjunto finito e ordenado possui um máximo

Então, definimos:

Máximo Divisor Comum de dois ou mais números, ao maior valor da interseção dos conjuntos dos divisores dos números dados.

Conteúdo deste artigo

Cálculo do MDC de vários números
1º Processo: decomposição em fatores primos
2º Processo: método das divisões sucessivas
3º Processo: método da decomposição simultânea
Máximo Divisor Comum de mais de dois números
Exercícios resolvidos

Cálculo do MDC de vários números

1º Processo: decomposição em fatores primos

Inicialmente, vejamos o que deve ocorrer com os fatores de um número D para que ele seja divisor de um outro número N. Assim, por exemplo, 6 é divisor de 30.

Como: 6 = 2 x 3 e 30 = 2 x 3 x 5,

Vemos que os fatores primos de 6 estão contidos nos fatores primos de 30.

Do mesmo modo, 9 é divisor de 54:

9 = 3² e 54 = 2 x 3³.

Também se vê que os fatores primos do número 9 estão contidos nos fatores primos de 54.

Já, por outro lado, 9 não é divisor de 24 e vê-se que:

9 = 3² e 24 = 2³ x 3.

Os fatores primos (3 x 3) do número 9 não estão contidos nos fatores primos (2 x 2 x 2 x 3) do número 24, que contém um só fator 3.

Então, podemos dizer:

Se D é divisor de N, então, os fatores primos de D devem estar contidos nos fatores primos de N.

Seja, então, calcular o m.d.c. (72, 120, 420)

Para facilitar a compreensão do conceito vamos apresentar inicialmente uma abordagem detalhada e descritiva para em seguida, mostrar o método prático.

D(72) = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}

D(120) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}

D(420) = {1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30, 35, 42, 60, 70, 84, 105, 140, 210, 420}

Os divisores comuns de 72, 120 e 420 são os elementos do conjunto

D(72) ∩ D(120) ∩ D(420) = {1, 2, 3, 6, 12) = D(12)

O maior desses divisores comuns (12) é chamado máximo divisor comum de 72, 120 e 420. Escrevemos: M.D.C (72, 120, 420) = 12

Em seguida, vamos apresentar o método prático, usando a decomposição em fatores primos.

Decompondo-se os números em fatores primos, obteremos:

72 = 2³ x 3²

120 = 2³ x 3 x 5

420 = 2² x 3 x 5 x 7

O número D – divisor comum de 72, 120 e 420 – deverá conter apenas os fatores primos comuns a 72, 120 e 420, para ser divisor dos três. Esses fatores primos comuns são os números 2 e 3. Todavia para ser o maior divisor comum devemos tomar 2² x 3¹ porque 2² está contido em todas as decomposições, assim como 3¹.

Para se calcular o M.D.C. de vários números, conclui-se a regra:

Decompõem-se os números dados em seus fatores primos.
Toma-se o produto dos fatores primos comuns a essas decomposições, cada um deles tomado com o menor dos expoentes que esse fator possui nas decomposições.

Exemplo:

Calcular o M.D.C. (816, 360).

816 = 2⁴ x 3 x 17

360 = 2³ x 3² x 5

M.D.C. = 2³ x 3¹ = 8 x 3 = 24

2º Processo: método das divisões sucessivas

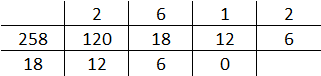
Para se achar o M.D.C. de dois números, divide-se o maior pelo menor. A seguir, divide-se o menor pelo resto da divisão entre o maior e o menor. A seguir, divide-se o 1º resto pelo 2º resto e assim sucessivamente. Quando se obtiver um resto zero, o último divisor é o M.D.C. procurado.

Exemplo:

Calcular o M.D.C. (258, 120)

3º Processo: método da decomposição simultânea

Nesse caso, a cada passo decomposição, vamos assinalar com “asterisco” cada fator que é divisor comum de todos os números à esquerda da linha do algoritmo.

Exemplo

Calcular o M.D.C. (420, 600).

O M.D.C. é dado pelo produto dos fatores que estão assinalados com “asterisco”.

M.D.C. (420, 600) = 2 x 2 x 3 x 5 = 60

Máximo Divisor Comum de mais de dois números

Calcular o M.D.C. (240, 180, 72, 54). Neste caso, utilizamos o método das divisões sucessivas em etapas, conforme podemos observar no esquema seguinte, onde chamamos de R₁ e R₂ os resultados parciais e R o resultado final.

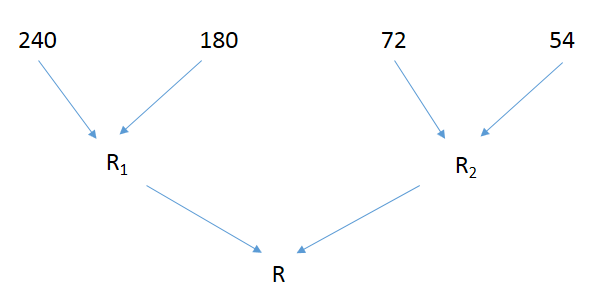
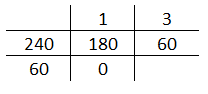
R₁ = 60

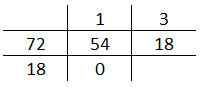
R₂ = 18

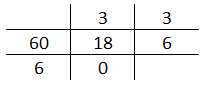
R = 6 ou

M.D.C. (240, 180, 72, 54) = 6

Exercícios resolvidos

1º) (ENEM) Um arquiteto está reformando uma casa. De modo a contribuir com o meio ambiente, decide reaproveitar tábuas de madeira retiradas da casa. Ele dispõe de 40 tábuas de 540 cm, 30 de 810 cm e 10 de 1 080 cm, todas de mesma largura e espessura. Ele pediu a um carpinteiro que cortasse as tábuas em pedaços de mesmo comprimento, sem deixar sobras, e de modo que as novas peças ficassem com o maior tamanho possível, mas de comprimento menor que 2 m.

Atendendo o pedido do arquiteto, o carpinteiro deverá produzir:

A) 105 peças.
B) 120 peças.
C) 210 peças.
D) 243 peças.
E) 420 peças.

Vamos obter o M.D.C. (540, 810, 1080) porque desejamos cortar as tábuas em pedaços iguais, sem deixar sobras, e atendendo ao requisito de que as novas peças tenham o maior tamanho possível.

Além disso, devemos observar que o comprimento de cada peça deve ser menor que 2m, ou seja, 200 cm.

O M.D.C. (540, 810, 1080) = 2 x 3 x 3 x 3 x 5 = 270 > 200

Para obter o comprimento de cada peça, devemos encontrar o maior divisor de 270 que é 135.

Dividindo cada tábua por 135 cm e multiplicando pela respectiva quantidade de tábuas de cada tipo, temos:

Tipo I: 540 ÷ 135 = 4 x 40 = 160

Tipo II: 810 ÷ 135 = 6 x 30 = 180

Tipo III: 1080 ÷ 135 = 8 x 10 = 80

Total de peças: 160 + 180 + 80 = 420

Resposta: letra E

2º) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos:

1) cada escola deverá receber ingressos para uma única sessão;

2) todas as escolas contempladas deverão receber o mesmo número de ingressos;

3) não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).

O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é:

A) 2
B) 4
C) 9
D) 40
E) 80

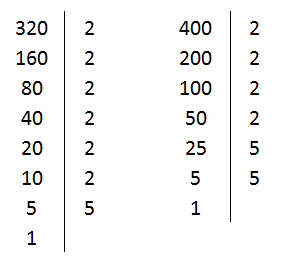
Pela decomposição dos números 320 e 420, temos:

320 = 2⁶ x 5

420 = 2⁴ x 5²

O M.D.C. (320, 420) = 2⁴ x 5 = 80 ingressos para cada escola

320 ÷ 80 = 4

400 ÷ 80 = 5

Portanto, o total de peças é 4 + 5 = 9

Resposta: letra C