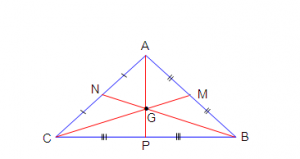
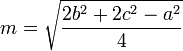A Mediana pode representar diversos fenômenos, porém dentro do contexto geométrico, ela é o segmento de reta que liga um vértice de um triângulo à metade (ponto médio) da aresta oposta a este ponto. Na figura abaixo temos representado as três medianas que podem existir em um triângulo, os segmentos de reta AP, BN e CM:
O ponto G da figura a cima representa o local onde as três medianas se interceptam e recebe o nome de baricentro (na Física, centro de gravidade ou centro de massa). Podemos equilibrar um triângulo, apoiando o seu baricentro em um alfinete ou palito, ele ficará estável!
Para calcularmos o tamanho da Mediana, podemos utilizar a seguinte fórmula; onde 'a' é o lado do triângulo que é tocado pela mediana, 'b' e 'c' são os demais lados e 'm' é o tamanho da mediana:
O ponto G divide a Mediana de maneira que o lado que toca o vértice é duas vezes maior que o lado que toca a aresta: AG = 2PG, BG = 2NG, CG = 2MG.
A Mediana divide qualquer triângulo em dois triângulos menores, de áreas iguais.
Em um triângulo retângulo, a Mediana que parte do ângulo reto divide a hipotenusa em dois segmentos de reta, do mesmo tamanho da mediana.
FONTES:
http://pt.wikipedia.org/wiki/Mediana_(geometria)
http://www.matematica.com.br/site/dicionario-matematica/87/210.html
Texto originalmente publicado em https://www.infoescola.com/matematica/mediana-geometria/