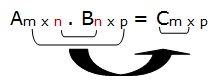Por Robison Sá
Neste trabalho, abordaremos a multiplicação entre matrizes, as suas particularidades e resolveremos algumas questões como forma de aplicação dos conceitos adquiridos ao longo deste estudo.
Conteúdo deste artigo
Definição
Dadas as matrizes A = (aij), de ordem m x n, e B = (bij), de ordem n x p, podemos obter a matriz produto C = A.B, do tipo m x p. Mas somente será possível encontrar a matriz produto C = (cij) se o número de colunas de A for igual ao número de linhas de B.
Em termos gerais, temos...
Exemplo 1
Dadas as matrizes 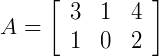 e
e 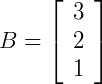 é possível encontrarmos a matriz produto a partir da multiplicação de A por B, pois o número de colunas de A é igual ao número de linhas de B. Porém, o produto B.A não é possível, visto que o número de colunas de B é diferente do número de linhas de A.
é possível encontrarmos a matriz produto a partir da multiplicação de A por B, pois o número de colunas de A é igual ao número de linhas de B. Porém, o produto B.A não é possível, visto que o número de colunas de B é diferente do número de linhas de A.
Para montarmos a matriz produto, devemos levar em conta que cada elemento da matriz Cij é obtido pela soma dos produtos de cada elemento da linha i de A pelo elemento correspondente da coluna j de B.
Em termos gerais, temos...
C = A . B = (cij)m x p
cij = ai1b1j + ai2b2j +...+ ainbnj
Isso significa dizer que para obtermos o produto de matrizes é preciso que multipliquemos cada elemento de uma linha pelo correspondente elemento de uma coluna somando os produtos obtidos em seguida.
Exemplo 2
Calcule 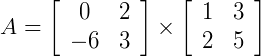 .
.
Resolução:
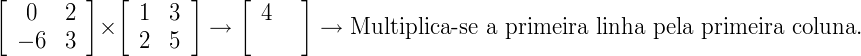
0 x 1 + 2 x 2 = 4
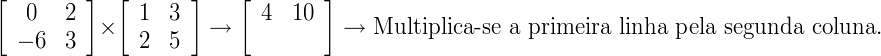
0 x 3 + 2 x 5 = 10
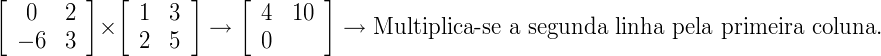
–6 x 1 + 3 x 2 = 0
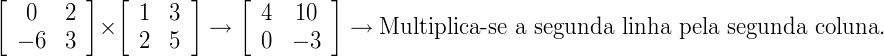
–6 x 3 + 3 x 5 = –3
Solução: 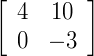
Propriedades da multiplicação de matrizes
- Associativa: (Am x n . Bn x p).Cp x r = A.(B.C)
- Distributiva: (Am x n + Bn x p).Cp x r = A.C + B.C e Am x n .(Bn x p .Cp x r) = A.B + A.C
- Elemento Neutro: Am x n .In = A e Im .Am x n = A, sendo I a matriz identidade.
- (k.Am x n).Bn x p = A.(k.B) = k.(A.B), com k ∈ R.
- (Am x n .Bn x p)t = Bt .At
Matriz Inversa
Dada a matriz quadrada A = (aij)n x n, dizemos que ela é inversível caso exista uma matriz B = (bij)n x n tal que:
A.B = B.A = In (matriz identidade)
Sendo B a matriz inversa de A, determina-se que B = A-1.
Exemplo 3
Multiplique a matriz 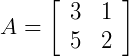 pela matriz
pela matriz 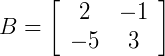 . O que quer dizer esse resultado?
. O que quer dizer esse resultado?
Resolução:
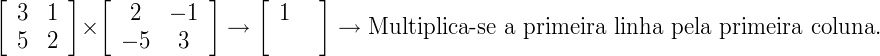
3 x 2 + 1 x (–5) = 1
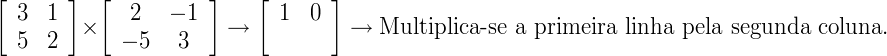
3 x (–1) + 1 x 3 = 0
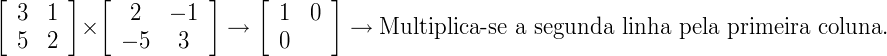
5 x 2 + 2 x (–5) = 0
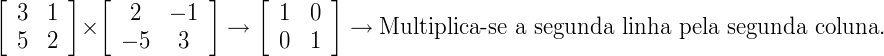
5 x (–1) + 2 x 3 = 1
Solução:  . Ao multiplicarmos A.B obtivemos a matriz identidade I2. Portanto, a matriz B é o inverso da matriz A (B = A-1).
. Ao multiplicarmos A.B obtivemos a matriz identidade I2. Portanto, a matriz B é o inverso da matriz A (B = A-1).
“Pegue carona na educação e conheça as maravilhas que o Universo tem a nos oferecer.”
(Robison Sá)
Referências bibliográficas
SOUZA, Joamir Roberto de. Novo Olhar Matemática. – 1 ed. – São Paulo: FTD, 2010. – (Coleção novo olhar; v. 2)
YOUSSEF, Antonio Nicolau. Matemática: ensino médio, volume único / Antonio Nicolau Youssef, Elizabeth Soares, Vicente Paz Fernandez. – São Paulo: Scipione, 2005.
Texto originalmente publicado em https://www.infoescola.com/matematica/multiplicacao-de-matrizes/