Um mesmo número pode ser representado de diferentes maneiras. Nesse artigo, vamos mostrar que os números decimais podem ser associados às frações decimais. Frações decimais são aquelas em que o denominador é uma potência de dez. É importante notar que um mesmo número pode ser representado na forma de fração ou na forma decimal.
Conteúdo deste artigo
Representação decimal
Observe o grande cubo abaixo e considere que ele representa uma unidade.
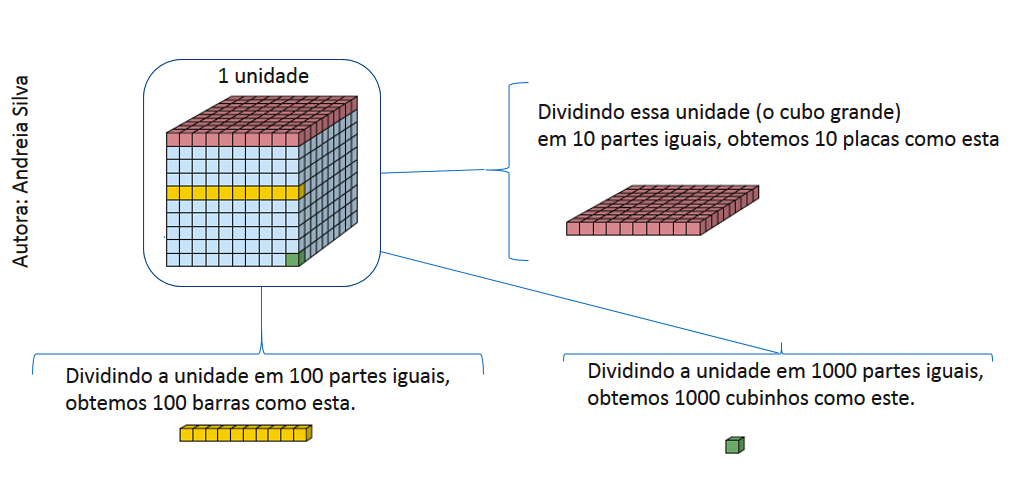
Unidade decimal
Toda fração decimal de numerador 1 é denominada unidade decimal. Assim:
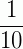é uma unidade decimal de 1ª ordem, que é representada por 0,1.
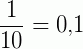→ um décimo
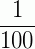é uma unidade decimal de 1ª ordem, que é representada por 0,01.
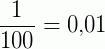→ um centésimo
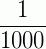é uma unidade decimal de 1ª ordem, que é representada por 0,001.
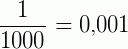→ um milésimo
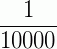é uma unidade decimal de 1ª ordem, que é representada por 0,0001.
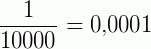→ um décimo de milésimo
... e assim por diante.
Leitura dos números decimais
Para ler um número decimal, consideramos primeiro a parte inteira e, em seguida, a parte decimal.
Exemplos:
- 3,8 três inteiros e oito décimos
- 12,005 doze inteiros e cinco milésimos
- 250,3 duzentos e cinquenta inteiros e três décimos
- 0,702 setecentos e dois milésimos
- 305,401 trezentos e cinco inteiros e quatrocentos e um milésimos
Da forma decimal para fracionária
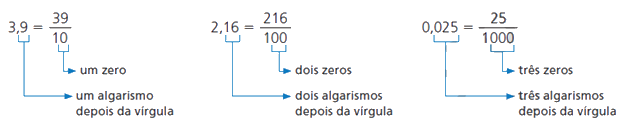
Primeiro retiramos a vírgula do número. Esse número, sem vírgula, será o numerador da fração. A seguir, no denominador, escrevemos uma potência de 10, na qual a quantidade de zeros é igual à quantidade de algarismos da parte decimal do número dado.
Comparar e ordenar números racionais na forma decimal
Vamos comparar e ordenar números decimais em uma reta numérica.
Como exemplo, vamos mostrar como ordenar os números: 6,25; 6,75 e 8,35.
Para conhecer o maior deles, basta olharmos para a parte inteira, o que tiver a maior parte inteira será o maior. Assim, verificamos que 8,35 é o maior entre os números.
Para descobrir qual é o maior entre 6,25 e 6,75, comparamos sua parte decimal. O que tiver o maior valor na parte decimal será o maior número. Assim, 6,75 é o maior que 6,25, pois 75 centésimos é maior que 25 centésimos.
Podemos afirmar que: 8,35 > 6,75 > 6,25
Outra maneira de dizer isso é:
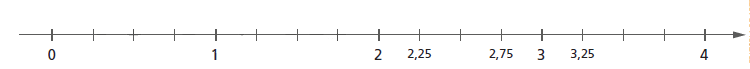
Note que, na reta numérica, quanto maior é o número, mais à direita ele está localizado.
Referências bibliográficas:
1. LIMA, E. L. Números e Funções Reais. Rio de Janeiro: SBM: Coleção PROFMAT, Sociedade Brasileira de Matemática, Rio de Janeiro, Brasil, 2013. 297 p.
2. LIMA, Elon Lages; CARVALHO, Paulo C. P.; WAGNER, Eduardo; MORGADO, Augusto C. A Matemática do Ensino Médio. vol. 1. Coleção do Professor de Matemática, SBM, 2012.
3. MOREIRA, Carlos T. de A.; SALDANHA, Nicolau C.; MARTINEZ, Fábio E. B. Tópicos em Teoria dos Números, Coleção PROFMAT, 2012. 1. MOREIRA, Carlos T. de A.; SALDANHA, Nicolau C.; MARTINEZ, Fábio E. B. Tópicos em Teoria dos Números, Coleção PROFMAT, 2012.
4. NETO, Antônio C. Muniz. Tópicos de Matemática Elementar, volume 1: Números Reais. Rio de Janeiro, Editora SBM, 2013.
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-decimais/