Conteúdo deste artigo
Complementar de um conjunto
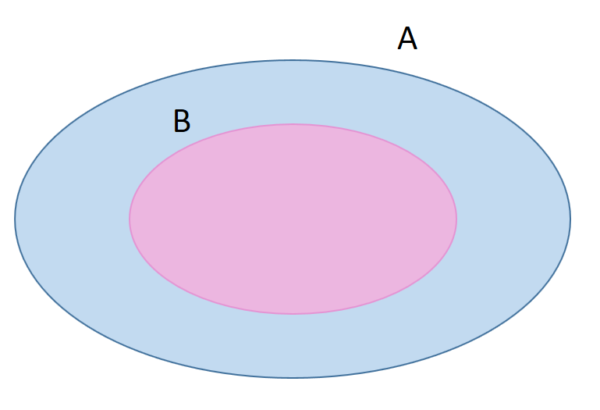
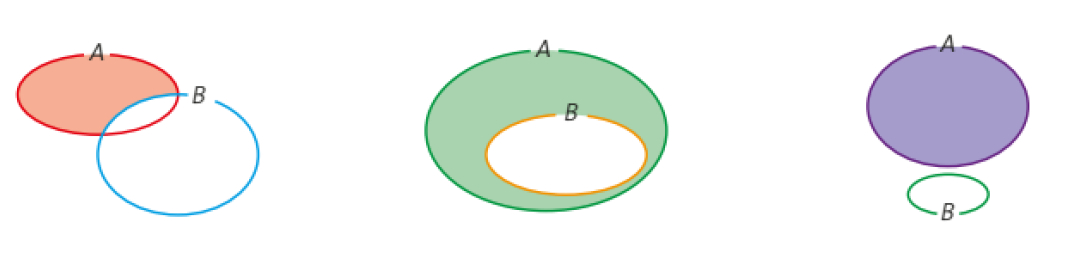
Dados dois conjuntos A e B, tais que o conjunto B ⊂ A chama-se complementar de B em relação a A, isto é, o conjunto dos elementos de A que não pertencem a B.
Com o símbolo 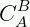 indicamos o complementar de B em relação a A.
indicamos o complementar de B em relação a A.
Notemos que 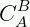 só é definido para B ⊂ A, e aí temos:
só é definido para B ⊂ A, e aí temos:
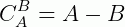
Exemplos
1º) Se A = {a, b, c, d, e} e B = {c, d, e}, então: 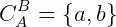
2º) Se A = {a, b, c, d} = B, então: 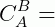
3º) Se A = {a, b, c, d} e B = 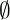 , então:
, então: 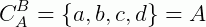
Propriedades da complementação
Sendo B e C subconjuntos de A, valem as seguintes propriedades:
1ª) 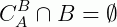 e
e 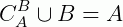
2ª) 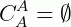 e
e 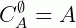
3ª) 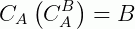 (complementar em relação a A do complementar de B em relação a A)
(complementar em relação a A do complementar de B em relação a A)
4ª) 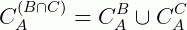
5ª) 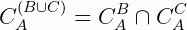
Reunião ou união de conjuntos
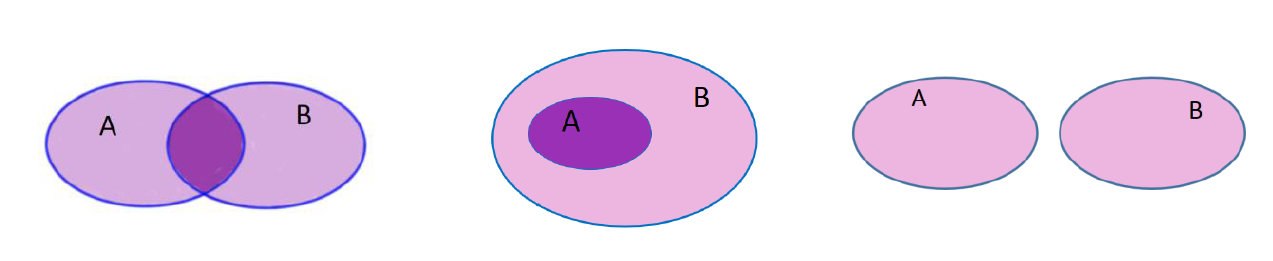
Dados dois conjuntos A e B, chama-se reunião de A e B o conjunto formado pelos elementos que pertencem a A ou a B.
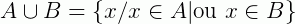
O conjunto 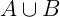 (lê-se: “ A reunião B ou “ A união B”) é formado pelos elementos que pertencem a pelo menos um dos conjuntos A e B.
(lê-se: “ A reunião B ou “ A união B”) é formado pelos elementos que pertencem a pelo menos um dos conjuntos A e B.
Notemos que x é elemento de 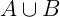 se ocorre ao menos uma das condições seguintes:
se ocorre ao menos uma das condições seguintes:
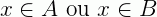
 Exemplos
Exemplos
1º) {a, b} ∪ {c, d} = {a, b, c, d}
2º) {a, b} ∪ {a, b, c, d} = {a, b, c, d}
3º) {a, b, c} ∪ {c, d, e} = {a, b, c, d, e}
4º) {a, b, c} ∪ ∅ = {a, b, c}
5º) ∅ ∪ ∅= ∅
Propriedades da reunião
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades:
1ª) A ∪ A = A (idempotente)
2ª) A ∪ ∅ = A(elemento neutro)
3ª) A ∪ B = B ∪ A (comutativa)
4ª) (A ∪ B) ∪ C = A ∪ (B ∪ C) (associativa)
Interseção de conjuntos
Dados dois conjuntos A e B, chama-se interseção de A e B o conjunto formado pelos elementos que pertencem a A e a B.
A ∩ B = {x / x ∈ A e x ∈ B}
O conjunto A ∩ B (lê-se: “ A interseção com B ou “ A inter B”) é formado pelos elementos que pertencem aos dois conjuntos (A e B) simultaneamente.
Se 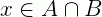 , isso significa que x pertence a A e também pertence a B. O conectivo “e” colocado entre duas condições significa que elas devem ser obedecidas simultaneamente.
, isso significa que x pertence a A e também pertence a B. O conectivo “e” colocado entre duas condições significa que elas devem ser obedecidas simultaneamente.
x ∈ A e x ∈ B
 Exemplos
Exemplos
1º) {a, b, c} ∩ {b, c, d, e} = {b, c}
2º) {a, b} ∩ {a, b, c, d} = {a, b}
3º) {a, b, c} ∩ {a, b, c} = {a, b, c}
4º) {a, b} ∩ {c, d} = ∅
5º) {a, b} ∩ ∅ = ∅
Propriedades da interseção
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades:
1ª) A ∩ A = A (idempotente)
2ª) A ∩ U = A (elemento neutro; U = conjunto Universo)
3ª) A ∩ B = B ∩ A (comutativa)
4ª) (A ∩ B) ∩ C = A ∩ (B ∩ C) (associativa)
Diferença de conjuntos
Dados dois conjuntos A e B, chama-se '''diferença entre '''A e B o conjunto formado pelos elementos de A que não pertencem a B.
A−B = { x / x ∈ A e x ∉ B}
Exemplos
1º) {a, b, c} - {b, c, d, e} = {a}
2º) {a, b, c} - {b, c} = {a}
3º) {a, b} - {c, d, e, f} = {a, b}
4º) {a, b} - {a, b, c, d, e} = ∅
Texto originalmente publicado em https://www.infoescola.com/matematica/operacoes-com-conjuntos/