O triângulo é uma das figuras mais importantes da geometria. Assim, conhecer seus elementos e seus pontos notáveis é um importante recurso que nos permite caracterizá-lo e encontrar várias relações importantes tanto para o estudo do triângulo quanto para o estudo de outras figuras. Vejamos os principais pontos notáveis de um triângulo:
Mediana
A mediana é um segmento de reta que parte de um dos vértices até o ponto médio do lado oposto a este vértice. Veja abaixo as possibilidades de medianas para um triângulo:
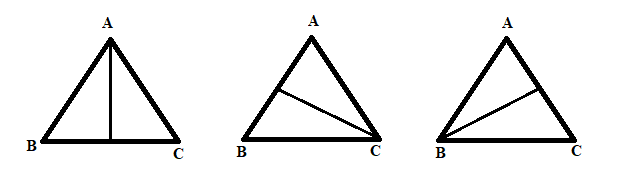
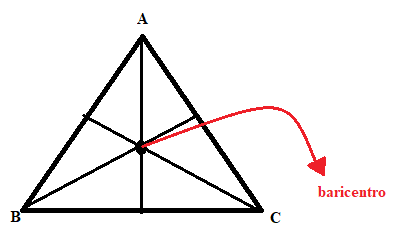
Quando traçamos as três medianas em um triângulo o ponto de encontro delas é chamado de baricentro.
Bissetriz
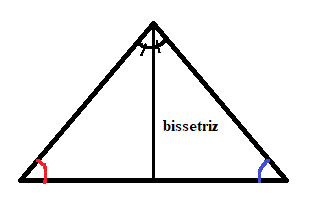
A bissetriz é o segmento que divide um ângulo interno em dois anglos congruentes.
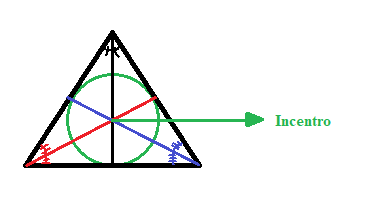
Quando traçamos as três bissetrizes encontramos um ponto de encontro entre elas, chamado de incentro. O incentro será o centro de uma circunferência inscrita que tangencia o triângulo nos três lados, ou seja, o centro dessa circunferência será equidistante dos três lados.
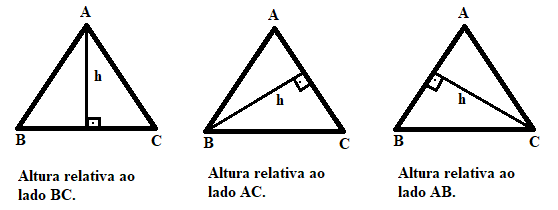
Altura
A altura é o segmento que parte de um dos vértices e é perpendicular ao lado oposto a este vértice.
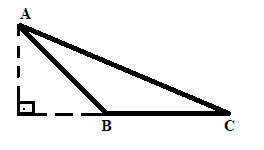
Quando o triângulo é obtusângulo a altura será externa ao triângulo, sendo necessário o prolongamento do lado oposto ao vértice.
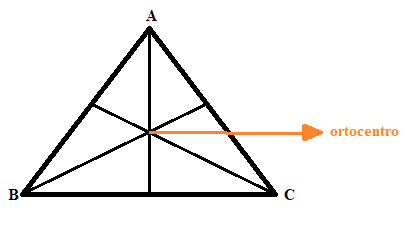
O ponto onde as três alturas se encontram é chamado de ortocentro.
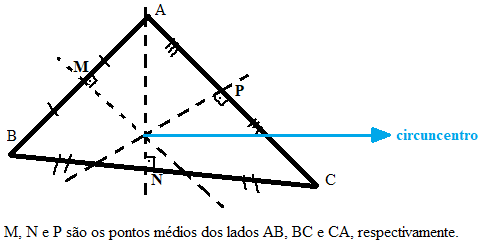
Mediatriz
A mediatriz é qualquer segmento de reta, que seja perpendicular a um lado e que passe no seu ponto médio.
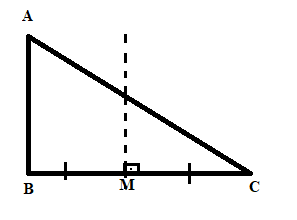
O ponto de encontro das três mediatrizes é chamado de circuncentro.
Leia também:
Referências:
NEVES, Elvis Donizete. Caracterização e localização dos pontos notáveis do triângulo. Tese de Mestrado apresentada como requisito para Mestrado Profissional de Matemática. Instituto de Ciências Matemática e Computação (ICMC). Universidade de São Paulo (USP). São Carlos, 2013.
FELINNI, Herlan; BATISTA, Pedro Tadeu; OKUHARA, Vitor. Matemática, teórico. Hexag Sistema de Ensino, volume 1, p. 75 e 76. São Paulo, 2020.
Texto originalmente publicado em https://www.infoescola.com/matematica/pontos-notaveis-de-um-triangulo/