Os produtos notáveis são uma forma de simplificar expressões algébricas. Eles são constantemente utilizados na matemática. Vamos agora mostrar os mais importantes:
- (𝑎+𝑏)1 = 𝑎 + 𝑏
- (𝑎+𝑏)2 = 𝑎2 + 2𝑎𝑏 + 𝑏2
- (𝑎+𝑏)3 = 𝑎3 + 3𝑎2𝑏 + 3𝑎𝑏2 + 𝑏3
- (𝑎+𝑏)4 = 𝑎4 + 4𝑎3𝑏 + 6𝑎2𝑏2 + 4𝑎𝑏3 + 𝑏4
- (𝑎+𝑏)5 = 𝑎5 + 5𝑎4𝑏 + 10𝑎3𝑏2 + 10𝑎2𝑏3 + 5𝑎𝑏4 + 𝑏5
- (𝑎+𝑏)6 = 𝑎6 + 6𝑎5𝑏 + 15𝑎4𝑏2 + 20𝑎3𝑏3 + 15𝑎2𝑏4 + 6𝑎𝑏5 + 𝑏6
Vamos expandir a expressão (𝑥+3)3 utilizando os produtos notáveis acima.
Note que nessa expressão, 𝑥 faz o papel de 𝑎 e 3 faz o papel de 𝑏 nos produtos notáveis, então, podemos dizer que,
(𝑥+3)3 = (𝑥 + 3) ∙ (𝑥 + 3)²
Então,
(𝑥 + 3)3 = (𝑥 + 3) ∙ (𝑥2 + 6𝑥 + 9)
(𝑥 + 3)3 = 𝑥3 + 9𝑥2 + 27𝑥 + 27
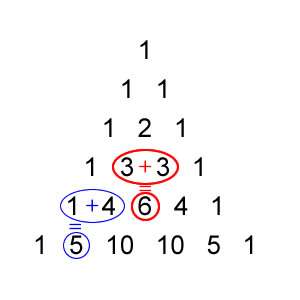
Uma curiosidade interessante desses produtos notáveis é que eles são casos especiais do teorema binomial. Seus coeficientes aparecem no chamado triangulo de Pascal.
Existem ainda, outros produtos notáveis que são importantes:
- Diferença de dois quadrados: 𝑎2 − 𝑏2 = (𝑎 + 𝑏)(𝑎 − 𝑏)
- Soma de dois quadrados: 𝑎2 + 𝑏2 = (𝑎 + 𝑏)2 − 2𝑎𝑏
- Soma de dois cubos: 𝑎3 + 𝑏3 = (𝑎 + 𝑏)(𝑎2 − 𝑎𝑏 + 𝑏2)
- Diferença de dois cubos: 𝑎3 − 𝑏3 = (𝑎 − 𝑏)(𝑎2 + 𝑎𝑏 + 𝑏2)
Vamos resolver alguns exercícios:
1) (UFC) Calcule o valor de 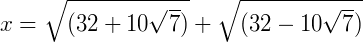 .
.
Podemos elevar ao quadrado ambos os lados da equação e a partir dai utilizar os conceitos de produtos notáveis. Vamos também dizer que os termos 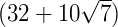 de a e
de a e 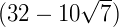 de b. Reescrevendo a equação:
de b. Reescrevendo a equação:
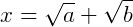
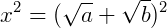
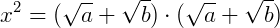
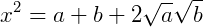
Agora, reinserindo os valores de 𝑎 e 𝑏:
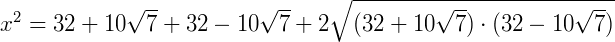
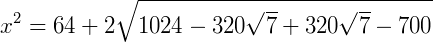
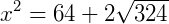
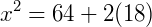
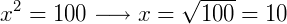
2) (IF-BA) Calcule o valor da expressão abaixo:
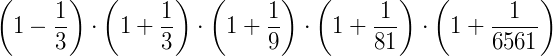
Este exercício é muito interessante. Se atribuirmos a igualdade 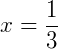 note que algumas potências de 𝑥 aparecem na expressão. Observe:
note que algumas potências de 𝑥 aparecem na expressão. Observe:
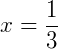
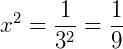
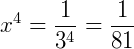
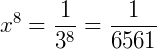
Então, convenientemente podemos fazer esta troca para continuarmos a calcular a expressão:
(1 − 𝑥) ∙ (1 + 𝑥) ∙ (1 + 𝑥²) ∙ (1 + 𝑥4) ∙ (1 + 𝑥8)
Agora, basta aplicar as regras de produtos notáveis, mais precisamente, a diferença de dois quadrados:
(1 − 𝑥²) ∙ (1 + 𝑥²) ∙ (1 + 𝑥4) ∙ (1 + 𝑥8)
(1 − 𝑥4) ∙ (1 + 𝑥4) ∙ (1 + 𝑥8)
(1 − 𝑥8) ∙ (1 + 𝑥8)
(1 − 𝑥16)
Agora basta reinserir o valor de 𝑥 que atribuímos. Logo, o valor da expressão é:
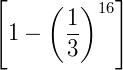
Existem ainda muitas aplicações envolvendo produtos notáveis. A ideia principal de usar esta ferramenta é identificar a estrutura da expressão, se ela coincidir com um produto notável, então é possível reduzir ou ampliar a expressão, dependendo da necessidade do problema.
Referências Bibliográficas
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/produtos-notaveis/