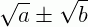Quando um radical ou uma expressão com radicais aparece como denominador de uma fração, é possível às vezes encontrar uma fração equivalente cujo denominador não contém radical. Tal procedimento é chamado racionalização de denominadores.
O processo geral consiste em multiplicar numerador e denominador por um fator conveniente, denominado fator racionalizante.
Vamos analisar os dois casos mais recorrentes.
1º caso: o denominador é um radical simples
O fator racionalizante é um radical com o mesmo índice que o denominador e com radicando tal que, ao se efetuar a multiplicação, a raiz obtida no denominador seja exata.
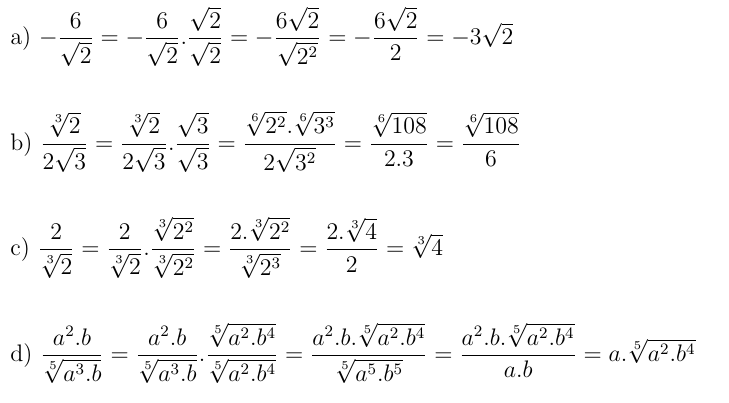
2º caso: o denominador é do tipo 
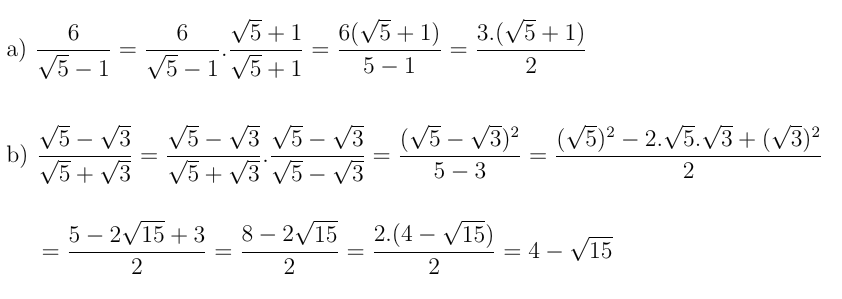
As vezes a racionalização deve ser feita por partes. Veja o exemplo a seguir.
Leia também:
Texto originalmente publicado em https://www.infoescola.com/matematica/racionalizacao-de-denominadores/