As razões trigonométricas são a base para o estudo da trigonometria e são obtidas pelas proporções dos lados de um triangulo retângulo. Como sabemos, um triangulo é retângulo quando um de seus ângulos é reto, ou seja, tem 90º:
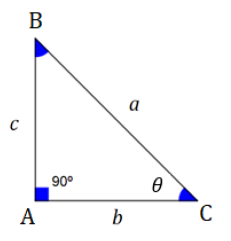
Num triangulo retângulo, o lado oposto ao ângulo reto (neste caso o lado BC cuja medida é igual a 𝑎, na figura) é chamado de hipotenusa. Já os outros dois lados, AB e AC, são chamados de catetos e têm medidas iguais a 𝑐 e 𝑏, respectivamente.
Lembrando também que, num triângulo retângulo vale o teorema de Pitágoras:
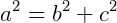
Agora, para obtermos as relações trigonométricas no nosso triangulo ABC precisamos inicialmente fixar um dos ângulos agudos. Veja, na figura, o ângulo 𝜃, evamos obter as relações trigonométricas com base neste ângulo:
Conteúdo deste artigo
Seno
O seno de um ângulo agudo é dado pela razão entre a medida do cateto oposto a ele e a medida da hipotenusa. Usando o ângulo 𝜃 como referência temos:
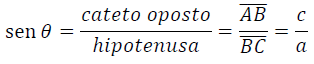
Cosseno
O cosseno é dado pela razão entre o cateto adjacente ao ângulo agudo e a hipotenusa. Com o ângulo 𝜃 teremos:
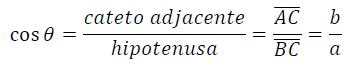
Tangente
Já a tangente é a razão entre o cateto oposto e o cateto adjacente do triangulo 𝐴𝐵𝐶, logo:
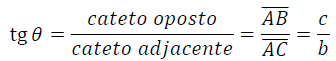
Existem ainda outras razões trigonométricas que podem ser obtidas pelas definições de seno, cosseno e tangente. Algumas delas, ainda fixando o ângulo 𝜃, são:
Cotangente
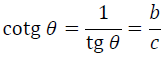
Secante
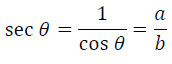
Cossecante
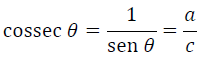
Relação Fundamental da Trigonometria
Ainda usando o nosso triangulo retângulo como exemplo, podemos obter, a partir do teorema de Pitágoras aquilo que chamamos de relação fundamental da trigonometria. Veja:
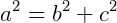
Como,
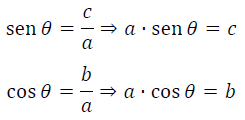
Podemos substituir 𝑐 e 𝑏, em função de seno e cosseno, na equação do teorema de Pitágoras:
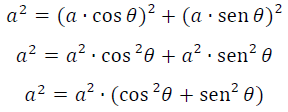
Por fim:
![]()
Que é a relação fundamental da trigonometria.
Senos, cossenos e tangentes de ângulos notáveis:
| 30º | 45º | 60º | |
| Seno |  |
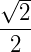 |
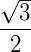 |
| Cosseno | 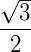 |
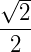 |
 |
| Tangente | 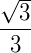 |
1 | 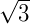 |
Texto originalmente publicado em https://www.infoescola.com/matematica/razoes-trigonometricas/