Toda expressão matemática que tenha forma 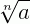 , com
, com 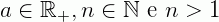 , recebe o nome de radical aritmético.
, recebe o nome de radical aritmético.
Em todo radical, podemos destacar:
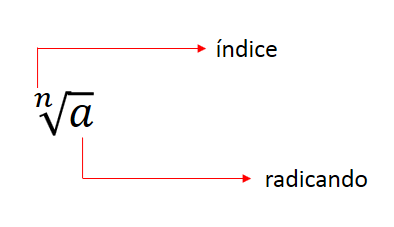
Assim:
No radical 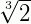 , o índice é 3, e o radicando é 2.
, o índice é 3, e o radicando é 2.
No radical 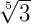 , o índice é 5, e o radicando é 3.
, o índice é 5, e o radicando é 3.
No radical 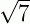 , o índice é 2 (=raiz quadrada, o índice é omitido), e o radicando é 7.
, o índice é 2 (=raiz quadrada, o índice é omitido), e o radicando é 7.
Simplificando radicais
Se um ou mais fatores do radicando têm o expoente igual ao índice do radical, de acordo com a propriedade 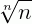 , esses fatores podem ser extraídos do radicando.
, esses fatores podem ser extraídos do radicando.
Em alguns casos, o expoente do radicando é maior que o índice do radical. Procura-se, então, fazer transformações convenientes no radicando, como você pode ver nas expressões abaixo.
Exemplo 1:
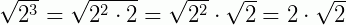
Exemplo 2:
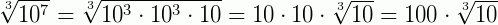
Exemplo 3:
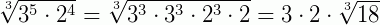
Exemplo 4:
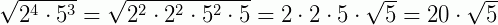
Há situações, porém, em que temos necessidade de fazer uma fatoração do radicando antes de realizar a extração dos fatores. Veja alguns exemplos.
1. Simplificar a expressão 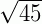 .
.
Fatorando o radicando 45, encontramos 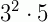 . Daí, temos:
. Daí, temos:
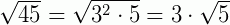
2. Qual é a forma mais simples possível de escrita da expressão 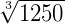 ?
?
Fatorando o radicando 1250, encontramos 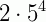 . Daí, temos:
. Daí, temos:
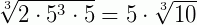
3. Sabendo que x e y são números reais positivos, simplifique a expressão 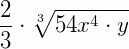
Fatorando o radicando 54, encontramos 54 = 2.33. Daí, temos:
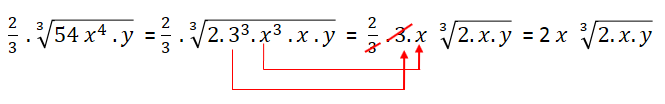
4. Simplifique a expressão:
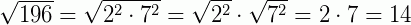
5. Simplifique a expressão:
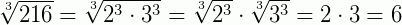
6. Simplifique a expressão:
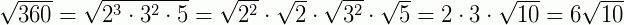
Leia também:
Texto originalmente publicado em https://www.infoescola.com/matematica/simplificacao-de-radicais/