Subtração de polinômios

Dados dois polinômios:

A(x) = a_n xⁿ + a_n-1 x^n-1 + ... + a₂x² + a₁x¹ + a_o

e

B(x) = b_n xⁿ + b_n-1 x^n-1 + ... + b₂x² + b₁x¹ + b_o

existe um único polinômio D(x) tal que

D(x) = A(x) - B(x) para todo 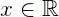. Esse polinômio é:

D(x) = (a_n - b_n) xⁿ + (a_n-1 - b_n-1 )x^n-1 + ... + (a₂ - b₂)x² + (a₁ - b₁)x¹ + (a_o - b_o)

e o denominamos diferença ou subtração de A e B. Indicamos: D = A - B

Exemplos:

1) Dados A(x) = x³ + 2x + 1 e B(x) = x² – 7x + 2, determinar o resultado da subtração de polinômios A(x) - B(x).

Para subtrair dois polinômios, devemos subtrair os coeficientes dos termos de mesmo grau, ou seja, os termos semelhantes. Quando faltar termo, devemos completar o coeficiente com zero.

A(x) - B(x) =

(x³ + 2x + 1) - (x² – 7x + 2) =

(1 - 0)x³ + (2 - 7)x + (1 - 2) =

x³ - 5x - 1

2) Dados A(x) = 7x³ + 2x² – 5x e B(x) = 2x³ – x² + 7x e C(x) = -x³ – 2x, determinar A(x) - B(x) - C(x).

A(x) - B(x) - C(x) =

(7x³ + 2x² – 5x) – (2x³ – x² + 7x) – (-x³ – 2x) =

[7 – 2 – (-1)]x³ + [2 – (-1) ] x² + [-5 – 7 – (-2)]x =

6x³ + 3x² -10x

3) Se P(x) = 3x⁴ – 5x + 4 e Q(x) = -x⁵ + 10x⁴ + 6x, então:

P(x) - Q(x) =

(3x⁴ – 5x + 4) - (-x⁵ + 10x⁴ + 6x) =

[0 – (-1)]x⁵ + (3 - 10)x⁴ + (-5 - 6)x + (4 – 0)

= x⁵ - 7x⁴ – 11x + 4

4) Dados P(x) = -5x⁶ -3x⁴ + 5x - 8 e Q(x) = -x⁶ + 4x⁵ – 9x + 10, temos:

P(x) - Q(x) =

(-5x⁶ -3x⁴ + 5x – 8) - (-x⁶ + 4x⁵ – 9x + 10) =

[-5 – (-1)]x⁶ + (0 - 4)x⁵ + [(-3) - 0)x⁴ + [5 – (-9)]x + (-8 - 10) =

-4x⁶ - 4x⁵ – 3x⁴ + 14x -18

5) Se P(x) = 2x³ – 3x + 1 e Q(x) = -2x³ + x² + 4, então:

P(x) - Q(x) =

[2 – (-2)]x³ + (0 - 1)x² + (-3 - 0)x + (1 - 4) =

4x³ – x² - 3x - 3

6) Dados A(x) = 7x³ + 2x² – 5x + 6 e B(x) = 5x³ – x² + 7x, determinar A(x) - B(x).

Para subtrair dois polinômios podemos adotar uma regra prática, que consiste em colocar os termos semelhantes numa disposição em forma de coluna. A seguir, devemos realizar a operação A(x) + [-B(x)], onde [-B(x)] é o polinômio oposto de B(x).

Vejam a seguir:

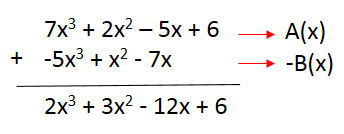
Para somar dois polinômios, devemos somar os coeficientes dos termos de mesmo grau, ou seja, os termos semelhantes. Quando faltar termo em algum dos polinômios, devemos completar o coeficiente com zero.

Leia também:

• Adição de polinômios
• Divisão de polinômios
• Multiplicação de polinômios
• Função polinomial
• Origem e importância dos polinômios

Referências bibliográficas:

1. LIMA, Elon Lages; CARVALHO, Paulo C. P.; WAGNER, Eduardo; MORGADO, Augusto C. A Matemática do Ensino Médio. vol. 3. Coleção do Professor de Matemática, SBM, 2012.

2. IEZZI, G.. Fundamentos De Matemática Elementar . Volume 6. 7ed. São Paulo: Atual Editora, 2004.

3. NETO, Antônio C. Muniz. Tópicos de Matemática Elementar: Volume 6. Polinômios. 2 ed. Rio de Janeiro: Editora SBM, 2016.