Teorema de Laplace

O teorema de Laplace nos traz uma forma generalizada para calcular o determinante de qualquer matriz quadrada. Para isso, recordemos o conceito de determinante de uma matriz.

Em resumo, o determinante é uma função matricial que associa a cada matriz quadrada a um escalar. Ou seja, o determinante transforma a matriz em um número.

Segue abaixo a definição formal do teorema de Laplace:

Seja M_n(K) o conjunto das matrizes quadradas (quando o número de linhas n for igual ao número de colunas) definida sobre um conjunto K,  e uma matriz A onde 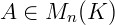, o determinante da matriz A, fixando a sua linha i ou a sua coluna j será dado por:

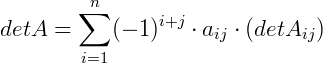
Em outras palavras: O determinante da matriz 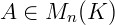é igual à soma algébrica do produto dos elementos de uma linha i ou de uma coluna j pelos seus respectivos cofatores .

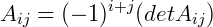Exemplo 1: Vamos calcular o determinante de uma matriz 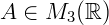, dada por:

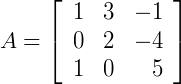
1º passo) Escolha uma linha ou uma coluna para fixar, por exemplo, a primeira linha;

2º passo) Identifique quais são os elementos da linha escolhida, que são:

• a₁₁ = 1
• a₁₂ = 2
• a₁₃ = -1

3º passo) Imagine que se selecionarmos cada elemento da nossa linha e excluir a linha e a coluna que ele pertence. Vemos que sobrará uma matriz menor, de ordem 2, veja abaixo:

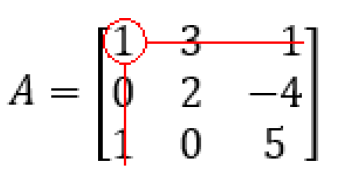
Esta matriz resultante da eliminação da linha e da coluna correspondente ao termo é a nossa matriz:

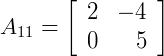
4º passo) Repetindo o 3º passo para os outros elementos da linha veremos que as matrizes resultantes das eliminações serão, em função dos termos a₁₂ e a₁₃:

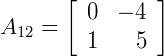
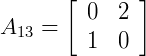
Calculando os determinantes das matrizes resultantes acima pelo método de Sarrus, temos que:

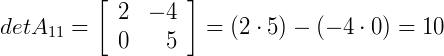
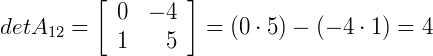
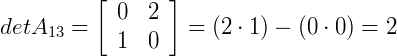
5º passo) Agora, calculando o somatório com a nossa 1ª linha, i = 1, fixada:

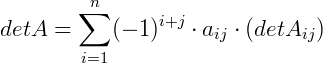
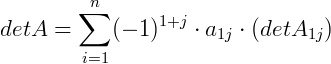
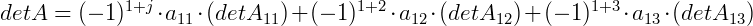
Como já temos todos estes valores, agora só nos resta calcular o valor do determinante:

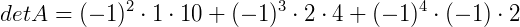
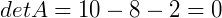
Provando o método de Sarrus

Com base neste teorema, podemos provar o método de Sarrus para calcular o determinante de uma matriz de ordem n em um conjunto K da seguinte forma:

Matrizes de Ordem 2: Seja 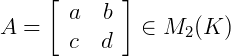. Por definição podemos dizer que o determinante de será:

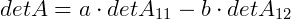
Como A₁₁ = d e A₁₂ = c, provamos o método de Sarrus, segue então que:

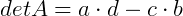
Matrizes de Ordem 3: Seja 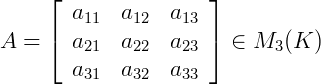, o seu determinante será dado por:

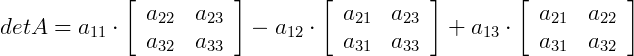
Que resultará em:

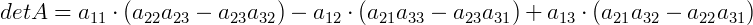
Se realizarmos as operações acima, temos:

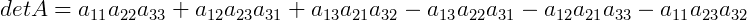
O que também prova que o método de Sarrus para calcular o determinante é uma recorrência do Teorema de Laplace.

Referências Bibliográficas:

COELHO, Flávio U; LOURENÇO, Mary L. Um Curso de Álgebra Linear. São Paulo: EDUSP, 2013

LIPSON, Marc; SEYMOUR, Lipschutz. Álgebra Linear. Porto Alegre: Bookman, 2011