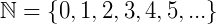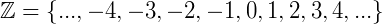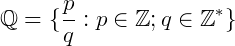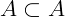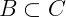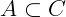Chamamos de conjunto toda e qualquer coleção de elementos. Estes elementos podem ser números, objetos, figuras, pessoas, animais e tudo o que podemos ordenar, catalogar ou reunir em grupos de seus elementos. Por exemplo: Se quisermos construir o conjunto de crianças de uma escola que possuam exatos 10 anos de idade, podemos dizer que o conjunto é composto pelos alunos Pedrinho, Joãozinho, Mariazinha, ..., e todos os alunos que tenham 10 anos de idade na escola. Matematicamente, quase sempre os conjuntos serão compostos por números e que dependam de algumas condições. Por exemplo: O conjunto dos números Reais, o conjunto dos números Inteiros, o conjunto dos números maiores do que 2 e menores do que 7, e muito mais.
A relação básica entre um conjunto e o elemento que o compõe é chamada de relação de pertinência, ou seja, definimos um conjunto quando existe uma regra que permite decidir se um elemento pertence ou não a ele. Se um elemento x pertence a um conjunto (ou coleção) A, dizemos que x pertence a A. Formalmente escrevemos:
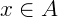
E quando x não é um elemento deste conjunto, dizemos que x não pertence a A:
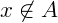
A maioria dos conjuntos em matemática não possuem uma definição para todos os seus elementos, logo a forma mais fácil de definir um conjunto é utilizando uma propriedade comum para todos os seus elementos, ou seja, uma lei que consiga ser associada a todos os elementos que o compõe. Vejamos abaixo alguns conjuntos numéricos usuais:
Exemplo 1: Vamos definir um conjunto A que seja construído a partir dos números Naturais e que qualquer elemento de A seja maior ou igual a 5 e menor ou igual a 10. Então o conjunto será:
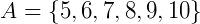
Como sabemos que qualquer elemento x que pertence a A é um número Natural neste exemplo, podemos representar o conjunto da seguinte maneira:
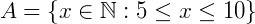
Lê-se: O conjunto A é igual a x (elemento qualquer de A) que pertence aos naturais, tal que 5 é menor ou igual a x e x é menor ou igual a 10 (ou x está entre 5 e 10).
Conteúdo deste artigo
Conjunto vazio
Existem alguns conjuntos que são representados por uma propriedade onde não é possível gerar elementos. Vejamos um caso:
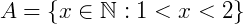
Note que qualquer elemento de A pertence ao conjunto dos naturais, porém é um absurdo dizer que nos naturais existem números entre 1 e 2, ou seja, em ℕ não existe o número 1,5, por exemplo. Então, neste caso, dizemos que o conjunto A é vazio. E será representado por:
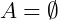
Atenção! O conceito de conjunto vazio remete a não existência de elementos, e não que o seu elemento é zero.
Subconjuntos
Note que no exemplo 1, os elementos do conjunto A estão contidos nos números Naturais, dizemos então que o conjunto A é um Subconjunto dos números Naturais, ou seja, o conjunto A está contido no conjunto ℕ. Escrevemos então:
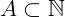
Exemplo 2: Basicamente, um subconjunto é um conjunto que possui elementos de outro. Como no exemplo da introdução, tomando o conjunto de crianças de 10 anos de idade em uma escola (chamaremos de A), e selecionando apenas os meninos (chamaremos de B), podemos dizer que o conjunto de meninos com 10 anos de idade é um subconjunto do conjunto das crianças. De uma maneira geral, dados dois conjuntos A e B, dizemos A é subconjunto de B quando todo elemento de A é também elemento de B. Sendo assim:
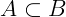
Exemplo 3: Os conjuntos numéricos ℕ, ℤ e ℚ cumprem uma relação de inclusão, onde:
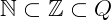
Propriedades da inclusão:
-
 (A sempre está contido em A);
(A sempre está contido em A); - Se
 e se
e se  então A = B ;
então A = B ; - Se
 e se
e se  então
então  .
.
Operações entre conjuntos
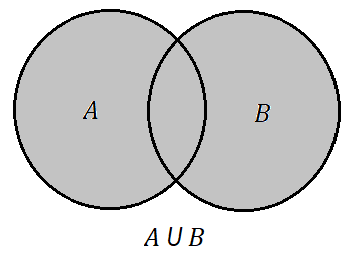
União de conjuntos: A união (ou reunião) de conjuntos é a junção dos elementos de um conjunto A mais ou elementos de um conjunto B. Podemos afirmar então que se um elemento x pertencer a união de A com B, então x pertence a A ou pertence a B. Formalmente definimos:
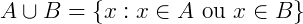
Veja abaixo uma representação no chamado diagrama de Venn. A região cinza simboliza a união dos seus respectivos elementos.
Interseção de conjuntos: A interseção de conjuntos é formada pelos elementos que são comuns entre A e B. Então:
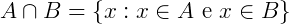
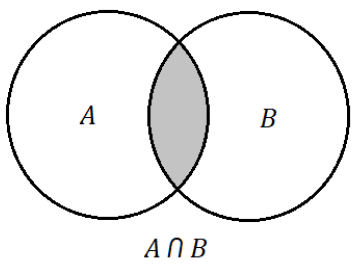
Propriedades:
| União |
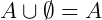 |
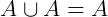 |
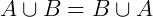 |
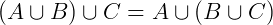 |
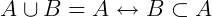 |
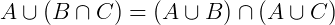 |
.
| Interseção |
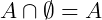 |
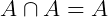 |
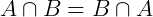 |
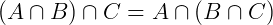 |
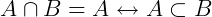 |
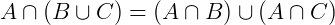 |
Conjuntos complementares
A diferença entre dois conjuntos A e B é o conjunto formado pelos elementos de A que não pertencem a B, formalmente dado por:
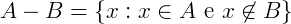
E representado no diagrama de Venn por:
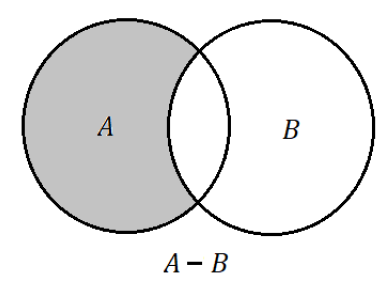
Não necessariamente B precisa estar contido em A para que exista A – B. Sendo assim, quando A ≠ B, nenhum elemento de A pertence a B, então A – B = A. Quando 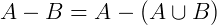 . Quando
. Quando 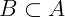 a diferença A – B se chama complementar de B em relação a A. Em notação formal dizemos:
a diferença A – B se chama complementar de B em relação a A. Em notação formal dizemos:
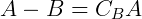
Relações binárias
Vamos supor que o conjunto A = {1,2} e o conjunto B = {3,4,5} com 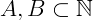 . O produto cartesiano A x B será dado por:
. O produto cartesiano A x B será dado por:
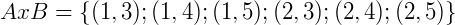
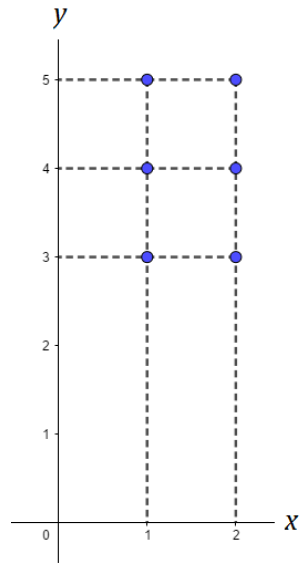
Se representarmos cada ponto de A x B geometricamente no plano cartesiano (ou também chamado de plano (x,y)) veremos que esta definição fica mais clara, pois todos os pontos do nosso exemplo serão indicados da seguinte forma:
Outro exemplo, um produto cartesiano dos números reais pelos reais, ou seja, 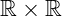 é o conjunto
é o conjunto 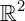 .
.
Leia também:
Referências Bibliográficas:
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.
MIRAGLIA, F. Teoria dos Conjuntos: Um Mínimo. São Paulo: EDUSP, 1992.
Texto originalmente publicado em https://www.infoescola.com/matematica/teoria-dos-conjuntos/