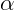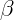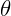O triângulo é uma das figuras geométricas mais simples que existem na Geometria. Apesar disso, foi alvo de inúmeros estudos no decorrer do desenvolvimento da Matemática ao redor do mundo. O estudo mais conhecido, talvez, é o Teorema de Pitágoras.
Conteúdo deste artigo
Definição de triângulo
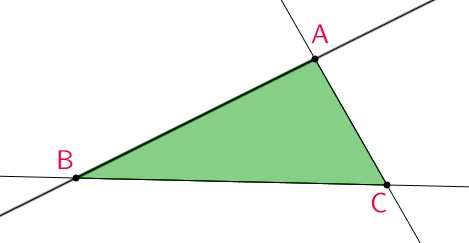
Formalmente falando, um triângulo é um polígono convexo. É a região formada por três semirretas concorrentes entre si, duas a duas a duas, em três pontos diferentes, formando seus três lados.
Outra definição sugere que, dados três pontos, A, B e C, não colineares (não alinhados), a reunião dos segmentos 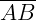 ,
, 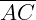 ,
, 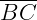 e chama-se triângulo ABC.
e chama-se triângulo ABC.
Elementos de um triângulo
Os elementos principais de um triângulo são: vértices, lado, altura e ângulo.
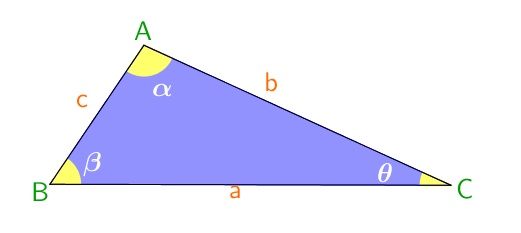
- Vértices: são os pontos de encontro das retas que formam o triângulo. Na figura, os vértices são os pontos A, B e C.
- Lados: são os segmentos que ligam um ponto a outro. Na figura, os lados são os segmentos a, b e c.
- Ângulo: Cada segmento forma uma “abertura” com outro, essa abertura é chamamos de ângulo interno. Assim, todo triângulo possui três ângulos internos, como visto na figura, representados por
 ,
,  e
e  .
. - Altura: A altura de um triângulo é o segmento que liga um ponto a seu segmento oposto (base), formando com ele um ângulo de 90°. Dizemos que a altura de um triângulo é sempre perpendicular à sua base.
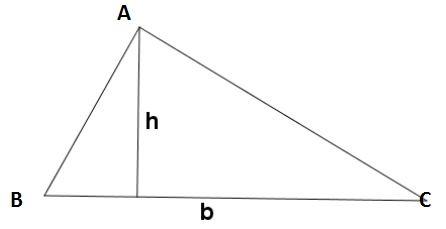
Altura h relativa ao lado BC.
Em alguns casos, a altura será da seguinte forma. Veja que, nesse caso, a altura h é relativa ao lado BC, que foi tida como base. Assim, devemos “prolongar” o lado BC e traçar uma perpendicular, partindo do vértice A.
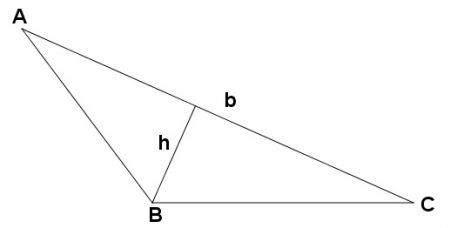
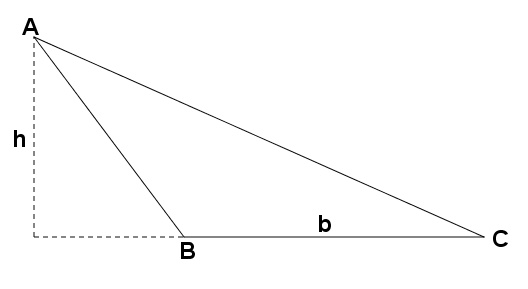 Caso a base escolhida seja o lado AC, teremos como altura, o segmento h, indicado na figura abaixo.
Caso a base escolhida seja o lado AC, teremos como altura, o segmento h, indicado na figura abaixo.
Classificação dos triângulos
Podemos classificar os triângulos de duas formas: quanto aos lados e quanto aos ângulos internos.
Classificação quanto aos lados
Quando consideramos os seus lados, um triângulo pode ser:
Escaleno
Um triângulo é escaleno quando nenhum de seus lados é congruente a nenhum outro, ou seja, todos os seus três lados são diferentes.
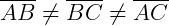
Isósceles
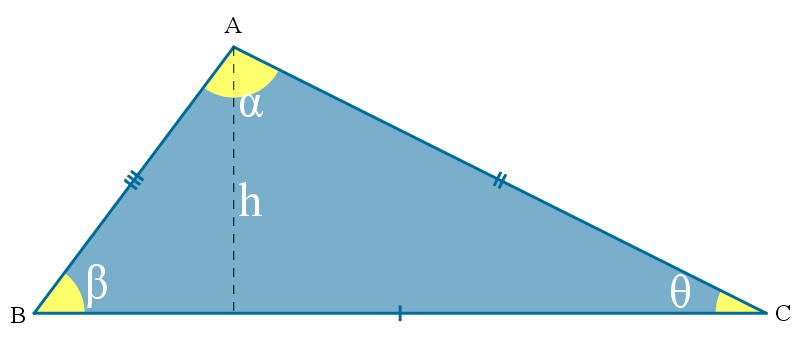
Um triângulo isósceles é aquele que apresenta sempre dois lados congruentes, ou seja, dois lados são sempre iguais e um é diferente.
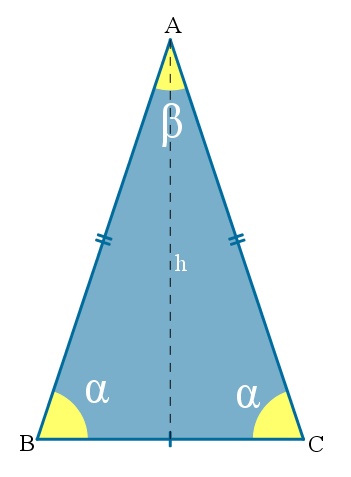
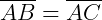
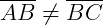
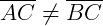
O lado diferente é usualmente chamado de base e o ângulo oposto a essa base é chamado de ângulo do vértice. Os ângulos opostos aos lados congruentes, também são congruentes, ou seja, os ângulos da base são sempre iguais.
No triângulo isósceles ABC acima, o lado BC é a base, A é o vértice, e o ângulo β é o ângulo do vértice.
No triângulo isósceles, o segmento da mediana, altura, mediatriz e bissetriz, serão sempre o mesmo, ou seja, coincidem. Mas apenas em relação à base.
Equilátero
Um triângulo equilátero é aquele cujo todos os seus lados são congruentes, ou seja, tem sempre a mesma medida (são iguais).
Sempre que um triângulo for equilátero, os três ângulos também serão congruentes, ou seja, terão a mesma medida. Essa medida é igual a 60°.
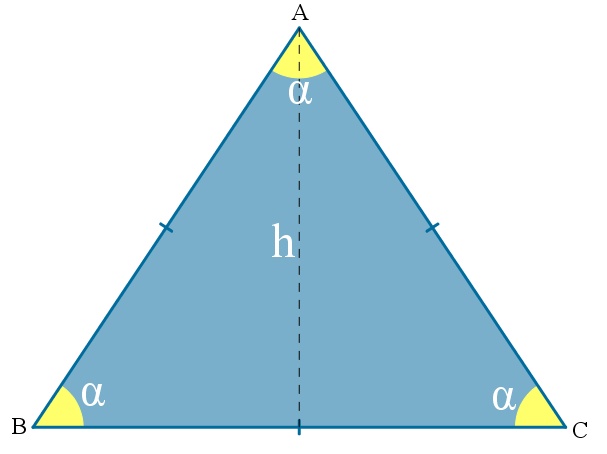
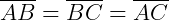
No triângulo equiláteros, o segmento que traça a mediana, a altura, a mediatriz e a bissetriz, será sempre o mesmo, ou seja, coincidem, independente do lado tomado como base.
Lembrando que a mediana de um triângulo é o segmento que parte de um vértice e divide o lado oposto a ele em duas partes iguais. A bissetriz é o segmento que parte de um vértice e divide seu ângulo em dois ângulos congruentes. A mediatriz é o segmento perpendicular a um dos lados, passando pelo seu ponto médio. A altura é o segmento que parte de um vértice e forma um ângulo de 90° com o lado oposto a esse vértice.
Classificação quanto aos ângulos
Quanto aos ângulos, um triângulo pode ser:
Acutângulo
Um triângulo será acutângulo se, e somente se, seus três ângulos internos forem agudos, ou seja, menores que 90°.
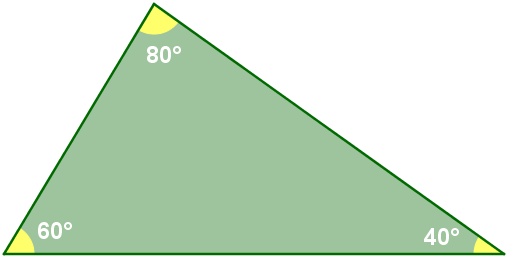
O triângulo acima é acutângulo, pois todos os seus ângulos são menores que 90°.
Obtusângulo
Um triângulo será obtusângulo se, e somente se, um de seus ângulos internos for obtuso, ou seja, maior que 90°.
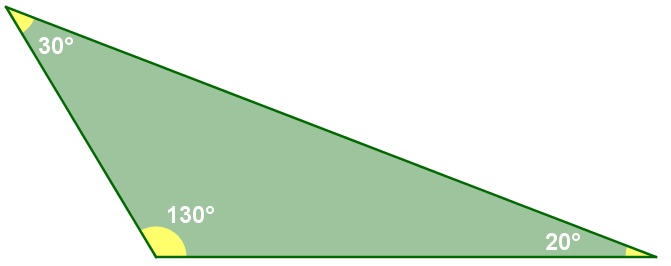
O triângulo acima é obtusângulo, pois possui um ângulo maior que 90°.
Retângulo
Um triângulo será retângulo se, e somente se, um de seus ângulos internos for reto, ou seja, exatamente igual a 90°.
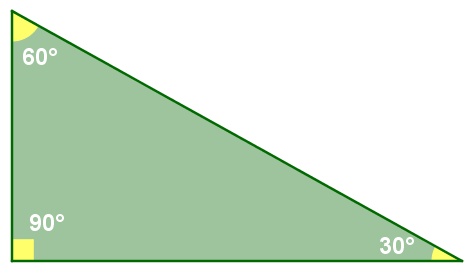
O triângulo acima é retângulo, pois possui um ângulo igual a 90°.
Nos triângulos retângulos, seus lados recebem nomes especiais. O lado oposto ao ângulo de 90° é chamado de hipotenusa e os seus outros dois lados são chamados de catetos.
Observações:
Uma classificação não exclui a outra. Um triângulo pode ser, por exemplo, um triângulo equilátero, isósceles ou escaleno também pode ser acutângulo.
Exercícios
1. Se o triângulo ABC é isósceles de base BC, determine x.
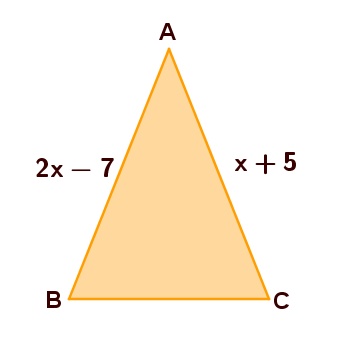
Se trata de um triângulo isósceles. Assim, os lados AB e AC são congruentes, ou seja, suas medidas são iguais:
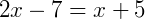
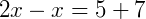
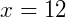
2. O triângulo ABC é equilátero. Determine x e y.
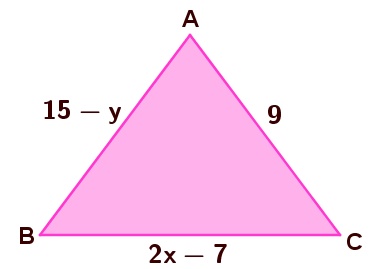
Se trata de um triângulo equilátero. Assim, os lados AB e AC e BC são congruentes, ou seja, suas medidas são iguais, assim, AB = AC = BC.
Fazemos AB = AC para encontrar y:
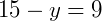
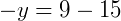
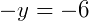
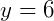
Fazemos BC = AC para encontrar x:
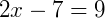
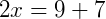
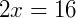
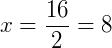
3. Classifique como verdadeiro ou falso
- Todo triângulo isósceles é equilátero.
- Todo triângulo equilátero é isósceles.
- Um triângulo escaleno pode ser isósceles.
- Todo triângulo isósceles é triângulo acutângulo.
- Todo triângulo retângulo é triângulo escaleno.
- Existe triângulo retângulo e isósceles.
- Existe triângulo isósceles obtusângulo.
- Todo triângulo acutângulo ou é isósceles ou é equilátero.
Respostas:
- FALSO: Nenhum triângulo isósceles é equilátero pois, por definição, um triângulo equilátero possui seus três lados congruentes, enquanto o isósceles possui apenas dois.
- VERDADEIRO: Se considerarmos dois lados do triângulo equilátero e o terceiro como uma base, este triângulo também será isósceles.
- FALSO: um triângulo escaleno, por definição possui todos os lados diferentes, logo dois lados nunca poderão ser iguais.
- FALSO: basta considerar um triângulo isósceles com ângulos da base medindo, cada um, 110°, por exemplo. Este triângulo será isósceles, mas como possui ângulos maiores que 90°, não é acutângulo.
- FALSO: basta considerar um triângulo onde os dois catetos têm a mesma medida. Quando isso acontece, teremos dois ângulos iguais medindo 45°, cada, o que torna esse triângulo escaleno.
- VERDADEIRO: considere o exemplo do item e.
- VERDADEIRO: considere o exemplo do item d.
- FALSO: um triângulo acutângulo possui os três ângulos agudos. Haverá casos em que os três lados serão todos diferentes, o que seria um triângulo escaleno. Assim, um triângulo acutângulo pode ser ou equilátero ou isósceles, mas também pode ser escaleno.
Referências:
DANTE, Luiz Roberto. Matemática. Vols: 1 a 3. São Paulo: Ática, 2004.
DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de Matemática Elementar. Geometria Plana. Vol: 9. São Paulo: Atual, 1995.
RIBEIRO, Paulo Vinícius. Matemática: Triângulos e pontos notáveis. Vol. 1. São Paulo: Bernoulli.
Texto originalmente publicado em https://www.infoescola.com/matematica/tipos-de-triangulos/