Quando trabalhamos com arcos trigonométricos ou com equações trigonométricas saber como reescrever alguns ângulos facilitam as manipulações algébricas e, por consequência, a resolução desses problemas. Assim, aprender formas de reescrever esses ângulos é de extrema importância e pode ser realizada utilizando as chamadas transformações trigonométricas.
Conteúdo deste artigo
Transformações trigonométricas: fórmulas de adição e subtração
Sejam a e b dois arcos trigonométricos, vejamos como escrever as transformações para o seno e o cosseno da soma desses ângulos:
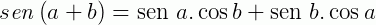
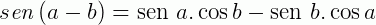
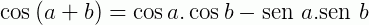
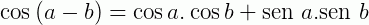
Para tangente também podemos escrever a soma e a subtração de dois ângulos a e b, porém, nesse caso temos uma restrição.
Para a soma, 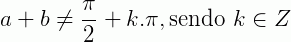 . Com isso temos que:
. Com isso temos que:
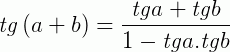
Para a subtração, 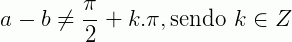 . Com isso temos que:
. Com isso temos que:
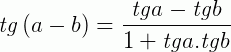
Exemplo
Determine 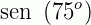 ,
, 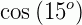 e
e 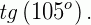
Solução:
Utilizando as relações apresentadas acima para 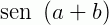 e
e 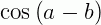 temos:
temos:
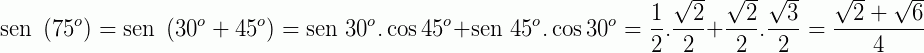
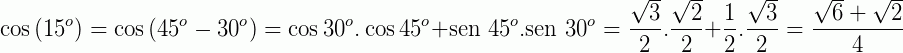
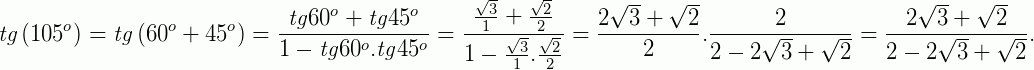
Transformações trigonométricas: fórmulas para o arco duplo
Seja o arco ‘a’, o arco duplo será composto por 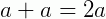 . Utilizando equações anteriores podemos chegar em:
. Utilizando equações anteriores podemos chegar em:
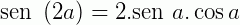
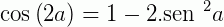
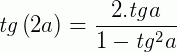
Transformações trigonométricas: fórmulas da metade do arco
Seja ‘a’ um arco trigonométrico, vejamos as transformações trigonométricas para metade dele, ou seja, para 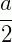 .
.
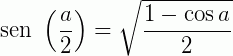
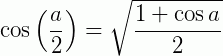
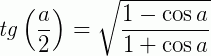
Exemplo
Seja 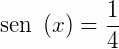 . Determine
. Determine 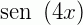 .
.
Solução:
Utilizando as fórmulas vistas acima, temos que
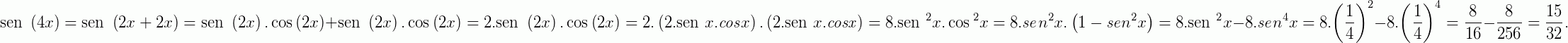
Logo, 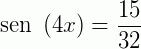 .
.
Fórmulas de Prostaférese
As chamadas fórmulas de Prostaférese são transformações usadas para fatorar expressões trigonométricas.
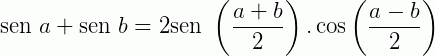
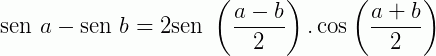
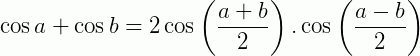
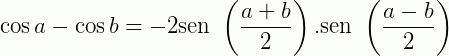
Exemplo
Fatores a expressão 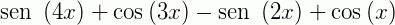 .
.
Solução:
Separando as partes com seno e cosseno, encontramos duas expressões:
* Separando só a parte dos senos e aplicando Prostaférese, onde a=4x e b=2x:
(I) 
* Separando a parte dos cossenos e aplicando Prostaférese, onde a = 3x e b = x:
(II) 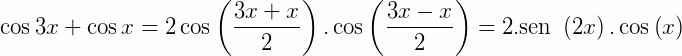
Juntando (I) e (II):
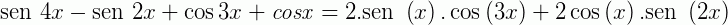
Referências:
KIHIAN, Kleber. Fórmulas de Prostaférese. Disponível em: https://www.obaricentrodamente.com/2009/07/formulas-de-prostaferese.html
Texto originalmente publicado em https://www.infoescola.com/matematica/transformacoes-trigonometricas/